A viga e a haste de aço são usadas para suportar a carga de . Se for exigido que a tensão normal admissível para o aço seja e a deflexão máxima não ultrapasse , determine o menor diâmetro da haste a ser usado. A viga é retangular, com de altura e de espessura.
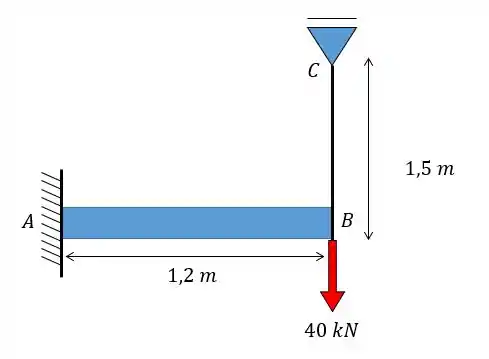
Passo 1
Galerinha linda, a primeira coisa que a gente precisa entender neste problema é que vão existir dois deslocamentos. Um referente à deflexão da viga e outro relacionado com a tração do cabo . Então, a gente pode representar num desenhozinho da seguinte maneira:
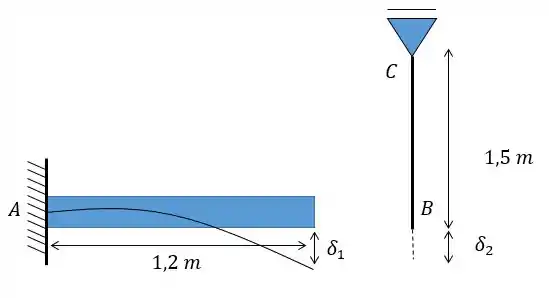
Por isso que faz total sentido utilizar o conceito de sobreposição, já que os deslocamentos estão sobrepostos, belezinha?
Além disso ambos estão localizados no ponto , logo, eles devem ser, necessariamente, iguais:
E vai ser por meio dessa realação que vamos conseguir resolver nosso probleminha. Partiu?
Passo 2
Pessoal, vamos começar pelo deslocamento da haste. Esse deslocamento depende das tensões trativas e é dado por:
Nós, temos , (aço ), a área depende do diâmetro que é o que queremos calcular. Você pode até achar que a força vale , mas não vale beleza? Não vale porque parte dessa força serve fletir a barra e parte para tracionar a haste. Então não temos por enquanto. Temos:
Mas repare que o problema nos diz que a tensão vale . Lembrando que:
A gente pode dizer que:
Passo 3
Para calcular a deflexão da viga a gente pode utilizar uma das nossas tabelas:
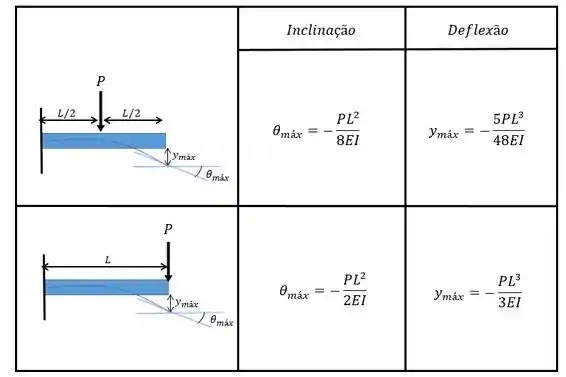
Logo, a deflexão será:
Vamos calcular o momento de inércia rapidinho:
Substituindo e lembrando que a força é igual à força aplicada de menos a parte relativa à haste nós vamos ter:
Repare que novamente não temos a força que atua. Mas pode ficar tranquilo que vamos encontrar essa força agora.
Passo 4
Como as duas deflexões são iguais nós vamos ter:
Então a força será igual a:
Agora é só substituir essa força na equação da tensão da haste:
Logo,