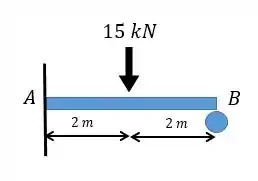
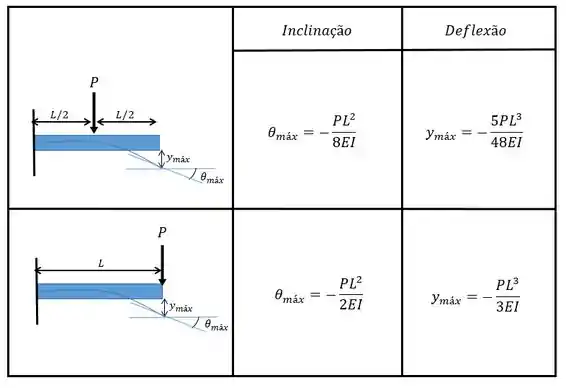
Determine as reações nos apoios e . Considere constante e utilize a tabela de deformações a seguir.
Passo 1
Faaaaala, galerinha MONSTRAAA da RESMAT!!!!Esse problema parece ser muito fácil já que ele pede somente as reações em e em , mas a gente tem que lembrar que se trata de uma viga estaticamente indeterminada, ou seja, uma viga hiperestática. Então, a gente não vai conseguir resolver simplesmente jogando aquelas equações da estática:
Porque a gente só vai ter três equações e temos, na verdade, 4 incógnitas. Então vamos resolver isso fazendo o método boladão da superposição que consiste em calcular as deflexões e achar relações entre elas para encontrar uma das 4 incógnitas isoladamente.
Então partiu resolver esse exercício!
Passo 2
Primeiramente vamos dividir o problema, como se a gente fosse resolver dois probleminhas isoestáticos separados. Para isso vamos retirar um dos apoios, mantendo a estrutura em equilíbrio!!! O apoio que vamos retirar vai ser a rótula e temos que adicionar a respectiva força de reação:
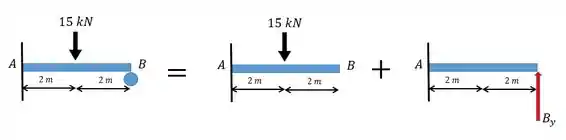
Passo 3
Agora vamos calcular a deflexão que cada componente, a força de e a força , realizam na barra. Para isso vamos desenhar um esquema de como fica a linha elástica de cada um desses elementos.
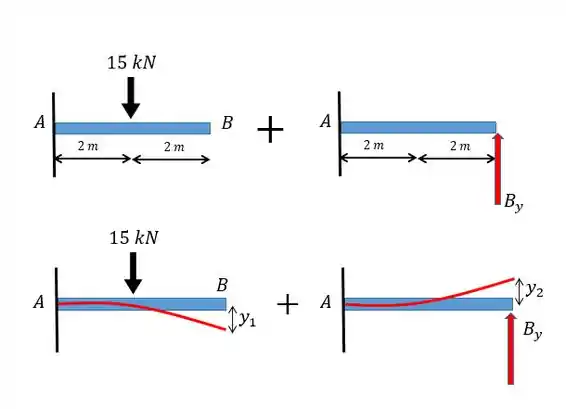
Nossaaaa que coisa mais linda, sério!

Então, pelo princípio da superposição a deflexão do ponto vai ser:
Então vamos calcular cada deflexão com auxílio da tabela fornecida. Para temos o primeiro caso, portanto:
Substituindo nós vamos ter:
Para nós temos o segundo caso:
substituindo:
É positivo mesmo, galera!! Veja que a força tem sentido oposto da tabela.
Passo 4
Agora a gente vai aplicar a equação da superposição que para este problema é igual a:
Aí agora que ta toda a sacaçãaumm desse problemitcho. Como a viga está apoiada em então nós vamos ter que a deflexão neste ponto vai ser igual a .
Então nós vamos ter:
Resolvendo essa equação a gente obtém:
Viram como a gente consegiu achar uma reação só com as propriedades na linha elástica?
Passo 5
Mas ainda faltam as reações em naõ é mesmo? Aí é só a gente utilizar as equações da estática mesmo...
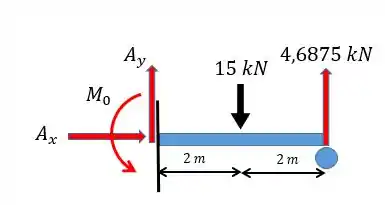
Fazendo a soma das forças em :
em
Para o momento:
E como dizem os franceses: VOUALA