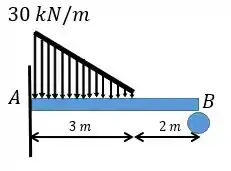
Determine a reação no apoio. Considere constante. Utilize a tabela fornecida.
Passo 1
Faaala pessoal!!! Vamos resolver essa questão sobre uma viga indeterminada, onde precisamos achar os valores das reações em , e . Mas para isso não basta utilizar apenas as equações da estática:
Porque a gente só vai ter três equações e temos, na verdade, 4 incógnitas. Então vamos resolver isso fazendo o método super neurótico da superposição que consiste em calcular as deflexões e achar relações entre elas para encontrar uma das 4 incógnitas isoladamente.
Então partiu resolver esse exercício!
Passo 2
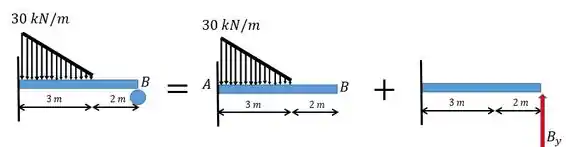
Primeiramente vamos dividir o problema, como se a gente fosse resolver dois probleminhas isoestáticos separados. Para isso vamos retirar um dos apoios, mantendo a estrutura em equilíbrio!!! O apoio que vamos retirar vai ser a rótula e temos que adicionar a respectiva força de reação:
Passo 3
Pessoal, fazendo um esboço da linha elástica
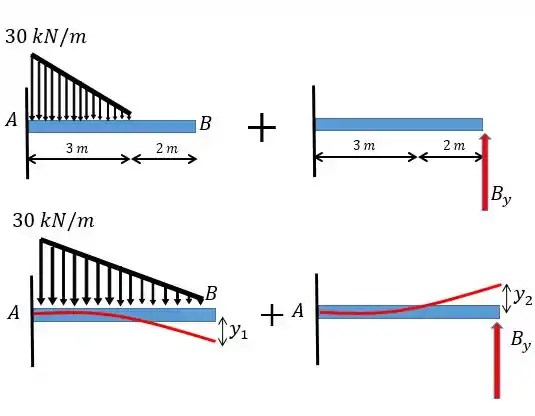
O que precisamos mesmo saber é que em a deflexão vai ser igual a zero por se tratar de um apoio, logo
Além disso pelo princípio da superposição a gente vai ter que:
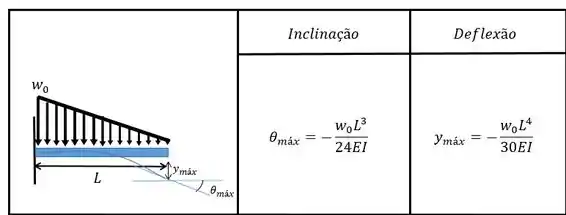
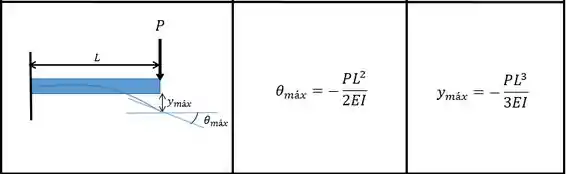
Então vamos calcular cada deflexão. Pessoal, a gente pode calcular da forma que acharmos melhor, qualquer método vale. Como normalmente para a aplicação deste método a tabela é utilizada vamos seguir com esse método.
Agora que vem umd detalhe importante, para calcular a deflexão devido a carga triangular a gente tem que utilizar um pouco de geometria e para isso vamos pegar a inclinação e multiplicar pela parte que está sem carga :
Enquanto para a força :
No caso da força a deflexão é positiva mesmo porque a força é de baixo para cima!
Passo 4
Agora vamos substituir essas deflexões na equação da superposição:
Substituindo os valores:
Agora vai A PARADA dessa questão que é perceber que não há deflexão em , por se tratar de um apoio, sendo assim .