Utilizando o método da superposição, determine o valor de em termos da carga dristribuída e da dimensão , de modo que a deflexão no centro da viga seja nula. é constante.
Passo 1
Fala, galerinha!!
Como o próprio enunciado já fala nós vamos ter de utilizar o método da superposição. Só para lembrar esse método consiste em calcular a deflexão que cada carga realiza num dado ponto e somar as deflexões de modo a obter a deflexão total.
Então primeiro nós precisamos achar a deflexão que carga realiza. Quando utilizamos a superposição nós quase sempre vamos utilizar as tabelas de deflexão, sendo assim vale lembrar da tabelinha:
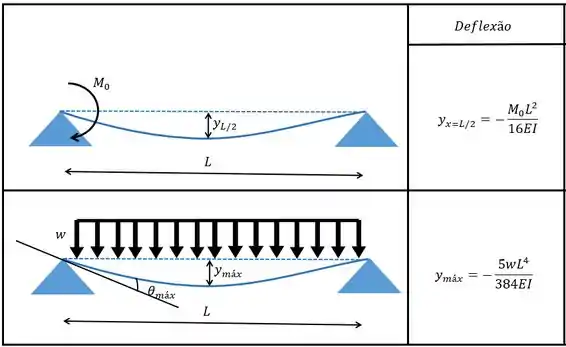
Repare que a deflexão relativa ao momento não é máxima no ponto médio ok? Então a gente não pode pegar o valor de , nos temos de pegar o valor de . Isso porque o problema quer que analisemos o centro da viga!
Show de bola, vamos resolver então!
Passo 2
Como nós temos três carregamentos: 2 momentos e uma carga distribuída, então nós vamos ter três deflexões que somadas devem dar a deflexão total:
Vamos calcular cada uma delas começando pela deflexão da carga distribuída:
Substituindo os valores:
Tranquilo né?
Passo 3
Agora vamos fazer para um dos momentos. Você deve ter reparado que existe uma pequena diferença entre a figura do problema e a figura da tabela. Na tabela o momento é colocado exatamente no apoio, enquanto no problema existe um afastamento.
Mas não se preocupe! Pois como se trata de um momento puro e nós queremos saber o que acontece entre os apoios, então podemos simplesmente ignorar a parte em balanço e fingir que esse momento atua exatamente no apoio. Obtendo:
Substituindo os valores:
Perceba que o valor da deflexão ficou positivo, isso porque o momento da nossa questão tem sentido inverso ao momento da tabela.
Além disso, como ambos os momentos são simpetricos então nós vamos ter que:
Passo 4
Agora é só somar as três deflexões:
Como o problema pede que a deflexão no centro seja nula: