Exercícios Resolvidos de Método dos Coeficientes Indeterminados – Soma de Funções
Ver TeoriaEnunciado
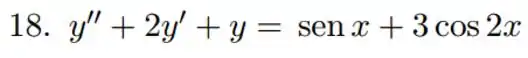
Passo 1
Encontrar solução homogênea:
Essa equação é simples de resolver. A equacao característica é:
Logo, as raízes são:
Assim, a solução homogênea é:
Passo 2
Encontrar com coeficientes a determinar:
Agora é uma soma de diferentes funções:
- Função trigonométrica:
- Função trigonométrica:
Então será também uma soma desses tipos de funções:
Passo 3
Verificar se a solução particular não é solução geral da equação homogênea:
Nessa EDO, essa solução não satisfaz a equação homogênea!
Passo 4
Encontrar derivadas de :
Passo 5
Substituir na equação e encontrar constantes:
Poderíamos substituir diretamente as derivadas e comparar os dois lados para encontrar as constantes:
Separando cada um dos coeficientes e igualando, temos que:
Assim, chegamos a:
Passo 6
Assim, a solução geral é da forma:
Resposta
Exercícios de Livros Relacionados
Encontre a solução geral da equação diferencial u ' ' + ω 0 2 u = c o s ω t Com ω 2≠ ω 0 2
Em cada um dos problemas de 15 a 20, encontre a solução do problema de valor inicial dado. y ' ' + 4 y = 3 sen 2 t , y 0 = 2 , y ' 0 = - 1
Em cada um dos problemas de 1 a 14, encontre a solução geral da equação diferencial dada. u ' ' + ω 0 2 u = cos ω 0 t
Encontre a solução geral da equação diferencialy^(' ') + 2 y^' + y = 2 e^(- t)
Encontre a solução geral da equação diferencialy^(' ') + y^' - 2 y = 2 t y (0) = 0 , y^' (0) = 1