Exercícios Resolvidos de Modelagem - MHS

Exercício 4 1 2 3 5 6

Enunciado

Um pendulo é formado prendendo-se uma haste longa e fina de complrimento e massa em um dado ponto, que está a uma distância acima do centro da haste. Encontre a equação diferencial do movimento e o período do pêndulo.

Passo 1

Primeiro vamos ver um esquema do pendulo descrito no enunciado:

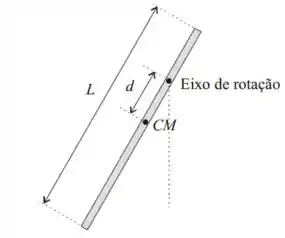
Assim, vamos equacionar esse problema.

Passo 2

Vamos usar a Segunda Lei de Newton para rotação:

Onde é o torque resultante, é o momento de inércia e é a aceleração angular.

Vamos calcular o torque em relação ao ponto do eixo, ou seja, o ponto que não se move:

Passo 3

Igualando as duas equações abaixo temos:

Como

Para pequenos valores de :

Então:

Passo 4

Assim, encontramos a equação do pêndulo. Mas calma essa equação é um MHS, né?

Vamos lembrar que no MHS podemos escrever:

Comparando as equações chegamos a:

Assim, o período de rotação é:

Resposta

Exercícios de Livros Relacionados

Mostre que o período do movimento de uma vibração não amortecida de uma massa pendurada em uma mola vertical é 2 π L / g , em que L é o alogamento da mola devido à massa, e g é a aceleração da gravida

A posição de um determinado sistema mola-massa satisfaz o problema de valor inicial 3 2 s ' ' + k s = 0 , s 0 = 2 , s ' 0 = v Se for observado que o período e a amplitude do movimento resultante são π

Na ausência de amortecimento, o movimento de um sistema mola-massa satifez o problema de valor inicial m s ' ' + k s = 0 ,s 0 = a ,s ' 0 = b (a) Mostre que a energia cinética dada inicialmente à massa

Suponha que uma massa m desliza sem atrito em uma superfície horizontal. A massa está presa a uma mola com constante k , como ilustrado na Figura 3.7 . 10 , e está sujeita, também,à resistência viscos

Nos problemas 3-8, escreva na forma 8 a solução para o problema de valor inicial dado.8. x ' ' + x = 0 ,x 0 = - 4 ,x ' 0 = 3