O sistema mostrado na Fig modela o braço de um mecanismo de elevação de peso. Determinar sua frequência natural de oscilação em torno do ponto .
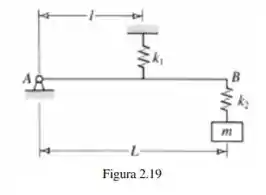
Passo 1
Primeiro vamos começar o problema, entendendo o que estamos buscando no problema e como vamos chegar à solução. Ok?
Pois bem, estamos buscando a frequência natural do - Movimento harmônico simples, mas que não é tão simples assim, não é mesmo rsrsrs. De acordo com a Teoria, se chegarmos a uma modelagem envolvendo uma EDO de 2º ordem como essa genérica aqui:
Então a frequência natural pode ser encontrada a partir do termo que multiplica . Então, basicamente devemos modelar o nosso problema e ver se a gente encontra algo parecido. Vamos nessa?
Passo 2
Para modelar o nosso problema, vamos basicamente utilizar em a física envolvida no nosso sistema: As Leis de Newton!
Considere então, o diagrama de forças livres no desenho a seguir:
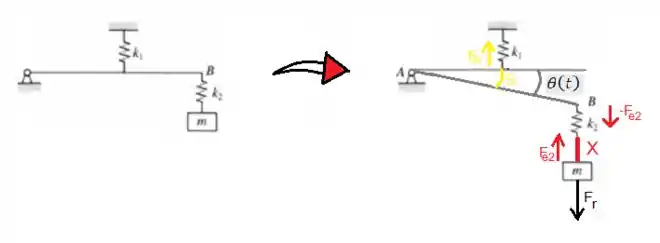
Na massa , temos basicamente a ação de duas forças: uma peso e outra proveniente da mola . Como a massa vibra, ela tem aceleração, logo tem força resultante. De acordo com as leis de Newton, a força resultante é a soma das duas únicas forças que atuam na mola:
Com isso temos a primeira equação. Agora, quero que você observe, também, que no problema, estamos trabalhando com rotações, então, também temos que encontrar uma equação para os torques!
Passo 3
As forças que causam torque na barra durante um tempo qualquer, é a resultante entre os torques causados pela mola 1 e pela mola 2 (duas únicas forças atuando sobre a barra):
Assim como a questão da força, devido ao fato da barra vibrar, tem aceleração, logo não podemos falar que a resultante é zero, saca?
Pronto, do sistema físico a gente tira duas equações:
Passo 4
Vamos estudar primeiro a primeira equação :
A força resultante é Newton mesmo: . A aceleração tem um detalhe importante que precisamos discutir: ela é a aceleração resultante da massa:
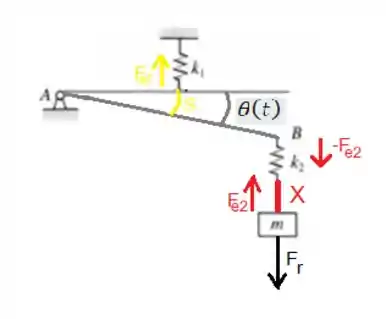
No caso, a massa têm dois deslocamentos: em vermelho e em verde. Como sabemos a aceleração resultante será a segunda derivada do deslocamento total em relação ao tempo:
O arco é dado pelo produto do raio pelo ângulo do arco:
Então...
Show! Agora vamos falar da força elástica : como qualquer força elástica...
A força peso, no entanto:
Então a gente conclui isso aqui:
Passo 5
Vamos estudar primeiro a segunda equação :
Novamente, vamos começar pela resultante: . Como estamos trabalhando com um sistema sem perdas de energia (característica de um MHS), podemos falar que o torque resultante em qualquer tempo, é o mesmo torque do início do movimento:
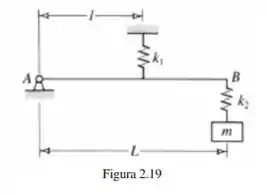
O legal de olhar o início, é que como as molas não estão esticadas, a única força que faz torque é o peso, então o torque resultante é:
O torque da mola , é o produto da força elástica pela distância de aplicação:
Lembrando que , onde é o arco amarelo de distorção da mola , dado pelo raio vezes o ângulo de distorção...
O torque da mola , por outro lado:
Esse menos é porque a força da mola que influencia no torque da barra é essa daqui:

Mas é a mesma coisa do passo anterior...
Então... Concluímos esse com:
Passo 6
Com os dois passos anteriores, nos chegamos nessas duas equações:
Vamos pegar essa segunda equação, isolar o (ou o porque tanto faz kkk):
Para substituir isso na primeira equação, vamos precisar da segunda derivada:
O primeiro termo dessa derivada é constante, logo sua deriva é ...
Calculando agora a segunda derivada...
Substituindo e na equação ...
Simplificando ainda mais...
Dividindo todo mundo que multiplica o para chegar à equação que a gente quer chegar...
Passo 7
Prontinho! Comparando então a EDO que acabamos de encontrar com a EDO geral de segunda ordem:
Concluímos que a frequência fundamental é:
Ou ainda: