Se o bloco tem um velocidade de para a direita, determine a velocidade do cilindro .
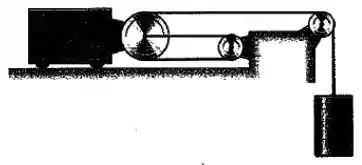
Passo 1
Pela geometria do sistema, podemos dizer que o comprimento total da corda pode ser aproximado por:
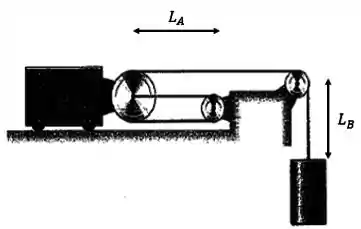
No entanto, temos que levar em consideração as “voltinhas” nas roldanas. Como não sabemos os diâmetros das roldanas, vamos dizer que será:
Onde é uma constante desconhecida (ela vai sumir nos próximos passos).
Passo 2
Derivando a expressão de em relação ao tempo, vamos ter que: