Para um dado valor de , determine a velocidade ascendente de em termos da velocidade descendente de . Despreze os diâmetros das polias.
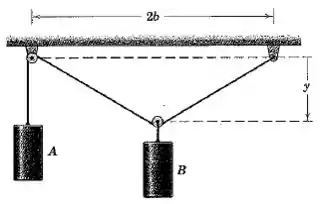
Passo 1
Vamos olhar o sistema:
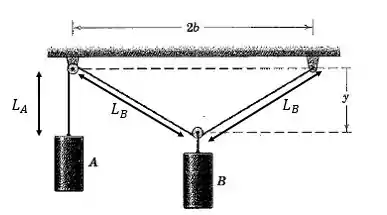
Assim:
Mas quem é
é:
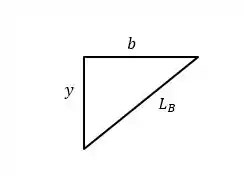
Assim:
E:
Passo 2
Derivando a expressão de :
Como derivar Devemos usar a regra da cadeia:
Assim:
Vamos chamar de