Em um dado instante, o cilindro tem uma velocidade para baixo de e uma aceleração para cima de . Determine a velocidade e a aceleração correspondentes do cilindro .
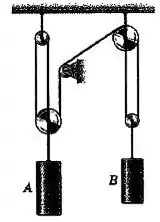
Passo 1
O sistema pode ser descrito por:
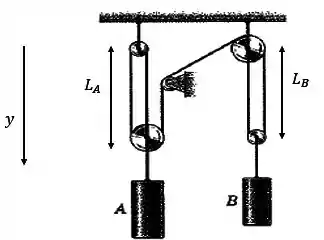
Observe que o sentido positivo do eixo aponta para baixo, ou seja, esse é o sentido positivo para o deslocamento.
A gente pode notar que existem dois comprimentos , certo?
Mas devemos computar quantos comprimentos ? Bom, de cara vemos 2... mas são
Naquela parte que existe uma roldana:
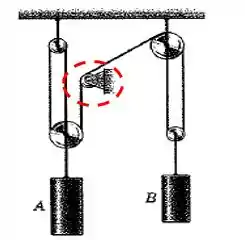
O comprimento da corda que vai de até a outra roldana tem, pelo menos, um valor . Assim, podemos dizer que:
Onde é a constante que engloba todos os comprimentos desconhecidos.
Passo 2
Assim, se derivarmos uma vez:
Derivando de novo:
Assim, a velocidade de será:
E a aceleração:
Por que é negativo? Porque está apontando para cima. Assim: