Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de e a velocidade de para um determinado valor de .
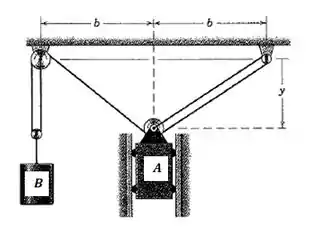
Passo 1
O sistema pode ser desenhado assim:
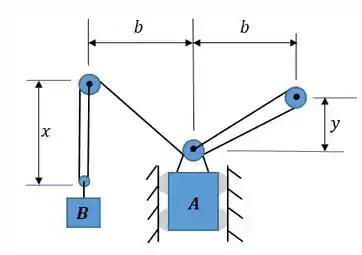
Passo 2
Assim:
Derivando essa expressão, temos que:
Adotando:
Então:
Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de e a velocidade de para um determinado valor de .

O sistema pode ser desenhado assim:

Assim:
Derivando essa expressão, temos que:
Adotando:
Então: