Encontre o valor da área do domínio plano situado no primeiro quadrante e limitado por , , .

Perceba que a região de integração é limitada por duas elipses, o que nos leva a pensar que utilizar coordenadas elípticas pode ser uma boa ideia. Vamos arrumar as equações de acordo com a forma geral da elipse para analisarmos melhor (o termo depois do “” dever ser ):

Repare que as elipses possuem coeficientes e diferentes entre si. Nesse caso, qual par e utilizaremos nas coordenadas elípticas? Não tem jeito, teremos que fazer substituições diferentes para cada curva. Vamos analisar a figura dessa região para entender melhor:

O que queremos é essa área em azul. Repare que ela é exatamente a diferença entre essas duas áreas em cinza:

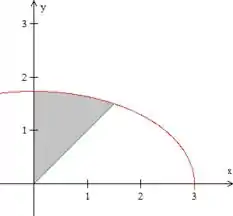
E

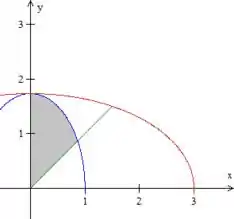
É assim que vamos calcular, então. Se calcularmos cada uma dessas áreas separadamente (e depois subtrairmos) podemos usar coordenadas elípticas diferentes.

Para a primeira área, limitada pela elipse de equação e pela reta , faremos:

Para a segunda, limitada pela elipse de equação e pela reta, faremos:

Agora que já decidimos as substituições, vamos calcular os intervalos de integração.

Para a primeira área: se substituirmos os valores que atribuímos a e a na elipse maior, teremos , pela própria definição que demos às coordenadas elípticas. Então, varia entre (origem do plano) e (equação da elipse). Para descobrir a variação de , temos que fazer a mudança de variáveis na equação da reta (pois ela que limita esse ângulo):

Pelo gráfico, vemos que o outro limite do ângulo é , o eixo . Você poderia também substituir , encontraria a mesma resposta.

Temos, então:

Para a segunda área: temos novamente para essa elipse (isso só ocorre porque estamos usando coordenadas diferentes!). O limite superior de é, também, . Para descobrir o inferior, vamos substituir os valores de e na equação da reta:

Temos, então:

Agora podemos montar a integral:

Vamos começar integrando em relação a :

Agora vamos integrar em relação a :