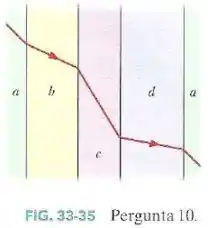
Na Fig.33-35 a luz começa no material , passa por placas feitas de três outros materiais com as interfaces todas paralelas entre si e penetra em outra placa do material .
A figura mostra o raio incidente e os raios refratados nas diferentes interfaces.
Coloque os materiais na ordem do índice de refração, começando pelo maior.
Passo 1
Quando um raio luminoso passa de um meio com índice de refração para um meio com índice de refração , temos:
Se, e somente se , o ângulo que o raio refratado faz com o vetor normal à interface dos meios é menor que o ângulo do raio incidente
Se, e somente se , o ângulo que o raio refratado faz com o vetor normal à interface dos meio é maior que o ângulo do raio incidente.
Logo, podemos comparar o índice de refração de duas placas em sequência pelo ângulo dos raios incidente e refratado.
Passo 2
Ao sair de e entrar em , o raio de luz faz um ângulo menor com a normal à superfície entre e . Por isso, .
De para o ângulo de refração é maior que o de incidência, e logo .
De para o ângulo decresce, o que significa que .
De para o ângulo cresce, indicando que
Passo 3
Agora temos um segundo problema:
Sabemos, por exemplo, que ambos e são maiores que e . Mas quem é maior entre e ?
A lei de Snell pode nos responder isso! Nesse caso, podemos aplica-la diversas vezes, o que nos dirá que:
Pois o âgulo de refração em será o mesmo que o incidente em e o de refração em será o mesmo que o de incidência em .
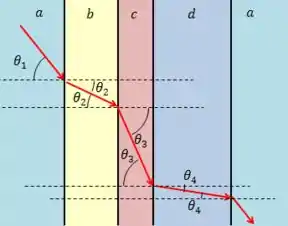
Isso nos diz que:
O que significa que, se o ângulo de refração em for maior que o em , , o e para os dois lados ficarem iguals, o índice de refração de precisaria ser menor que o de .
Porém o ângulo de refração em é menor que o de , o que nos diz que . Podemos fazer o mesmo para e :
E sendo o ângulo de refração em maior que o incidente entre e , isso significa que .
Por esse raciocínio, juntando todos os passos: