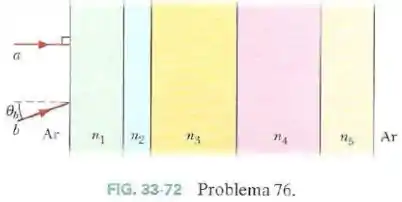
Na Fig.33-72 dois raios luminosos que estavam se propagando inicialmente no ar passam por cinco placas de plástico transparente e voltam para o ar. As placas têm interfaces paralelas e espessura desconhecida; os índices de refração são , , , e .
O ângulo de incidência do raio é . Em relação à normal à última interface, determine:
- O ângulo de saída do raio .
- O ângulo de saída do raio .
- Do raio .
- Do raio .
(Sugestão: Pode ser mais rápido resolver o problema algebricamente.)
Se em vez de ar houver um vidro com um índice de refração à esquerda e à direita das placas, determine o ângulo de saída:
Passo 1
Letra a)
Quando o raio passa de um meio para outro perpendicular à interface, o raio propagado no segundo meio também vai ter uma direção normal à interface.
Por isso o raio vai atravessar todas as placas perpendicular às interfaces, e acabará saindo no fim com o mesmo ângulo no ar.
Logo, seu ângulo de saída é zero.
Passo 2
Letra b)
Como as interfaces de todas as placas são paralelas, podemos usar a lei de Snell consecutivas vezes usando o mesmo ângulo para dois usos em sequência.
Se usarmos apenas os dois extremos da equação:
Sendo os dois ângulos menores que , podemos dizer que
O ângulo de saída será igual ao de entrada .
Passo 3
Letra c)
Se invés de ar, tivéssemos vidro dos dois lados, nosso raciocínio para um raio perpendicular seria o mesmo.
Logo, o ângulo de saída do raio continuaria sendo zero.
Passo 4
Letra d)
Novamente, o raciocínio se mantém, e o ângulo de saída será igual ao de entrada.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)