Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Múltiplas Refrações

Ver Teoria
Exercício 412356

Enunciado

Na Fig.33-59 um feixe luminoso que se propaga inicialmente no material 1 é refratado para o material 2 , atravessa esse material e incide com o ângulo crítico na interface dos meios 2 e 3 .

Os índices de refração são n 1 = 1,60 , n 2 = 1,40 e n 3 = 1,20 .

  1. Qual é o valor do ângulo θ ?
  2. Se o valor de θ aumenta, a luz consegue penetrar no meio 3 ?

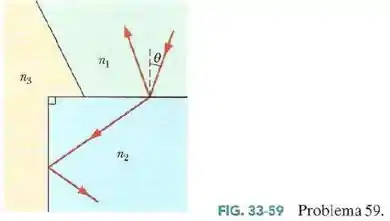
Passo 1

Letra a)

O raio que incide no material 2 com um ângulo θ é refratado com um ângulo dado pela lei de Snell

n 1 sen ⁡ θ = n 2 sen ⁡ θ 2

sen ⁡ θ = n 2 sen ⁡ θ 2 n 1

Agora precisamos encontrar θ 2 .

Passo 2

Podemos ver que temos um triângulo retângulo formado pelo raio refratado no meio 2 e o ponto onde a luz incide nas interfaces entre 1 e 2 e entre 2 e 3 . Com isso, podemos encontrar o ângulo de incidência na interface entre 2 e 3 .

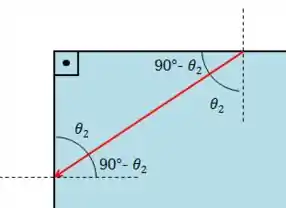
Usando a lei de Snell:

n 2 sen ⁡ 90 ° - θ 2 = n 3 sen ⁡ θ 3

Mas pelo enunciado, 90 ° - θ 2 é o ângulo crítico, o que significa que θ 3 = 90 ° , e também:

  • n 2 = 1,40
  • n 3 = 1,20

A trigonometria também nos diz que sen ⁡ 90 ° - θ 2 = cos ⁡ θ 2 .

cos ⁡ θ 2 = n 3 n 2 = 1,2 1,4 ≅ 0,857

θ 2 ≅ cos - 1 ⁡ 0,857 ≅ 31 °

Passo 3

Substituindo na nossa primeira equação junto com n 1 = 1,60 :

sen ⁡ θ = n 2 sen ⁡ θ 2 n 1 ≅ 1,4 ∙ sen ⁡ 31 ° 1,6 ≅ 0,451

θ ≅ sen - 1 ⁡ 0,451 ≅ 26,79 °

Passo 4

Letra b)

Se θ aumentar, θ 2 aumenta e 90 ° - θ 2 diminui, diminuindo o ângulo de refração θ 3 e possibilitando que a luz penetre no meio 3 .

Resposta

Letra a)

θ ≅ 26,79 °

Letra b)

Sim, se o valor de θ aumenta a luz consegue penetrar no meio 3 .

Exercícios de Livros Relacionados

• Uma estudante de física jogando bilhar deseja atingir a bola branca de forma que ela atinja a tabela e, então, a bola oito diretamente. Ela escolhe vários pontos na tabela e, então, mede a distância
Na Fig. 33-51, a luz incide, fazendo um ângulo 81 = 40,1º com a normal, na interface de dois meios transparentes. Parte da luz atravessa as outras três camadas transparentes e parte é refletida para c
Na figura 33-65, um raio luminoso entra em uma placa de vidro no ponto A, com um ângulo de incidência θ 1 = 45,0 ° , e sofre reflexão interna total no ponto B. De acordo com essas informações, qual é
(a) Prove que um raio de luz que incide em uma janela de vidro emerge do lado oposto com uma direção paralela à do raio original e um deslocamento lateral como na figura 33-69. (b) Mostre que, para pe
Suponha que o ângulo do vértice superior do prisma de vidro da fig 33-53 seja ϕ = 60 ° e que o índice de refração do vidro seja n = 1,6 . (a) Qual é o menor ângulo de incidência θ para o qual um raio