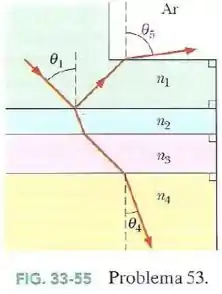
Na Fig.33-55 a luz incide, fazendo um ângulo com a normal, na interface de dois materiais transparentes. Parte da luz atravessa as outras três camadas transparentes e parte é refletida para cima e escapa para o ar.
Se , , , e , determine o valor:
- De
- De
Passo 1
Letra a)
Pela lei da reflexão, o raio refletido na interface de com terá o mesmo ângulo que o ângulo de incidência.
Como ele incide em uma interface paralela a essa entre e o ar, o ângulo de incidência nesse plano será o mesmo que o de reflexão.
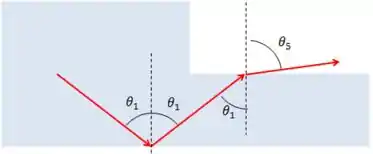
Usando a lei de Snell:
Sabemos que , e pelo enunciado:
Passo 2
Letra b)
As interfaces são todas paralelas e nós podemos usar a lei de Snell para dizer:
Ou seja:
O índice de refração de é .
Resposta
Letra a)
Letra b)
Exercícios de Livros Relacionados
• Uma estudante de física jogando bilhar deseja atingir a bola branca de forma que ela atinja a tabela e, então, a bola oito diretamente. Ela escolhe vários pontos na tabela e, então, mede a distância
Na Fig. 33-51, a luz incide, fazendo um ângulo 81 = 40,1º com a normal, na interface de dois meios transparentes. Parte da luz atravessa as outras três camadas transparentes e parte é refletida para c
Na figura 33-65, um raio luminoso entra em uma placa de vidro no ponto A, com um ângulo de incidência θ 1 = 45,0 ° , e sofre reflexão interna total no ponto B. De acordo com essas informações, qual é
(a) Prove que um raio de luz que incide em uma janela de vidro emerge do lado oposto com uma direção paralela à do raio original e um deslocamento lateral como na figura 33-69. (b) Mostre que, para pe
Suponha que o ângulo do vértice superior do prisma de vidro da fig 33-53 seja ϕ = 60 ° e que o índice de refração do vidro seja n = 1,6 . (a) Qual é o menor ângulo de incidência θ para o qual um raio