Exercícios Resolvidos de Operações com matrizes

Enunciado

É possível fazer as seguintes multiplicações?

Passo 1

Para começarmos precisamos lembrar que para multiplicar duas matrizes, é preciso que: o número de colunas da primeira matriz seja igual ao número de linhas da segunda.

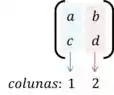
Vamos começar contando o número de colunas da primeira matriz, podemos ver que ela tem duas.

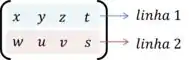
Agora vamos contar o número de linhas da segunda matriz, podemos observar facilmente que ela possui duas linhas.

Como a quantidade de colunas da primeira matriz é igual a de linhas da segunda matriz, podemos fazer essa multiplicação.

Passo 2

Seguindo a mesma ideia, a primeira matriz é igual a da letra a do exercício e possui 2 colunas.

Só que agora a segunda matriz possui 3 linhas.

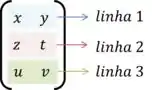
Como esses valores são diferentes, não podemos realizar essa multiplicação.

Resposta

Sim
Não

Exercícios de Livros Relacionados

Em cada um dos Problemas 25 e 26, verifique se a matriz dada satisfaz a equação diferencial dada.25. Ψ ' = 1 1 4 - 2 Ψ,Ψ t = e - 3 t e 2 t - 4 e - 3 t e 2 t

Em cada um dos problemas de 22 a 24, verifique se o vetor dado satisfaz a equação diferencial dada.22. x ' = 3 - 2 2 - 2 x, x = 4 2 e 2 t

Se A ( t ) = ([[e^t,2,e^(- t),e^(2 t)],[2,e^t,e^(- t),-,e^(2 t)],[-,e^t,3,e^(- t),2,e^(2 t)]]) e B ( t ) = ([[2,e^t,e^(- t),3,e^(2 t)],[-,e^t,2,e^(- t),e^(2 t)],[3,e^t,-,e^(- t),-,e^(2 t)]]) , encontr

Em cada um dos problemas de 22 a 24, verifique se o vetor dado satisfaz a equação diferencial dada.24. x ' = 1 1 1 2 1 - 1 0 - 1 1 x,x = 6 - 8 - 4 e - t + 2 0 1 - 1 e 2 t

Verifique se o conjunto abaixo é espaço vetorial real, com as operações usuais. No caso afirmativo, exiba uma base e dê a dimensão. a ) Matrizes diagonais n × n .