Seja a matriz
Calcule
Passo 1
Vamos lembrar que , ou seja, vamos calcular:
Para multiplicar duas matrizes, vamos lembrar-nos da nossa frase: “Linha por coluna”.
Vamos fixar a primeira linha da primeira matriz, e vamos multiplicar pela primeira coluna para descobrir o nosso primeiro elemento.
Continuando com a primeira linha fixada, vamos multiplicar pela segunda coluna:
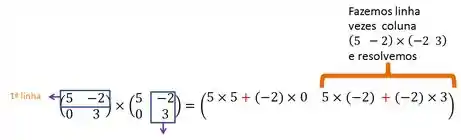
Passo 2
Passo 3
Agora, fixamos a segunda linha e multiplicamos pela primeira coluna:
Agora a segunda linha, com aa segunda coluna:
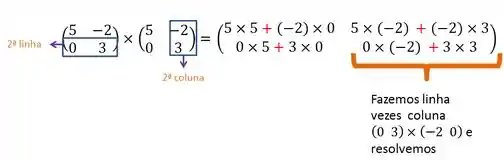
Passo 4
Assim, temos:
Resposta
Exercícios de Livros Relacionados
Em cada um dos Problemas 25 e 26, verifique se a matriz dada satisfaz a equação diferencial dada.25. Ψ ' = 1 1 4 - 2 Ψ,Ψ t = e - 3 t e 2 t - 4 e - 3 t e 2 t
Em cada um dos problemas de 22 a 24, verifique se o vetor dado satisfaz a equação diferencial dada.22. x ' = 3 - 2 2 - 2 x, x = 4 2 e 2 t
Se A ( t ) = ([[e^t,2,e^(- t),e^(2 t)],[2,e^t,e^(- t),-,e^(2 t)],[-,e^t,3,e^(- t),2,e^(2 t)]]) e B ( t ) = ([[2,e^t,e^(- t),3,e^(2 t)],[-,e^t,2,e^(- t),e^(2 t)],[3,e^t,-,e^(- t),-,e^(2 t)]]) , encontr
Em cada um dos problemas de 22 a 24, verifique se o vetor dado satisfaz a equação diferencial dada.24. x ' = 1 1 1 2 1 - 1 0 - 1 1 x,x = 6 - 8 - 4 e - t + 2 0 1 - 1 e 2 t
Verifique se o conjunto abaixo é espaço vetorial real, com as operações usuais. No caso afirmativo, exiba uma base e dê a dimensão. a ) Matrizes diagonais n × n .