Se de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
(a)
(b)
(c)
(d)
(e) Nenhume das alternativas
Passo 1
E aí, tudo bem?
Já que a base é quadrada, queremos uma caixa mais ou menos assim:
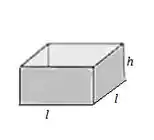
O enunciado também nos deu que estão disponíveis de material para fazer essa caixa.
A nossa restrição então é que a área total dela é 1200.
Vamos colocar em linguagem matemática...
Passo 2
A área total dessa caixa é dada pela soma das áreas de cada pedacinho.
Temos a base, que é:
E temos 4 laterais retangulares, medindo por , ou seja:
A área total vai ser a soma da área da base mais as áreas laterais. Então ela será dada por:
E como a área total é 1200, temos:
Ok, segura isso por enquanto!
Passo 3
Vamos lá, a gente quer encontrar o maior volume possível pra caixa, dentro da condição que a gente viu ali em cima.
O volume da caixa (que é um paralelepípedo) é calculado assim:
Vamos colocar isso em função de uma variável só usando a condição que achamos ali em cima.
Passo 4
A gente pode isolar o nessa expressão aqui pra deixar em função de :
Vamos substituir na fórmula do volume agora:
Simplificando o :
Passo 5
Beleza, agora que temos a função a ser maximizada em termos de uma variável só. Podemos partir para a derivada:
Agora, vamos igualar a zero para encontrar os pontos críticos:
Como estamos falando de medidas, ficamos só com o valor positivo .
Passo 6
Ok, agora é só acharmos o valor de que acompanha esse e depois calcular o volume!
E então o volume máximo possível é:
Alternativa (a) 😊