Determine a área máxima possível de um triângulo retângulo de hipotenusa .
Passo 1
Como queremos a área máxima possível, temos um problema de otimização!
Nosso primeiro passo sempre é organizar as informações que temos do enunciado e, sempre que possível, fazer um desenho.
Queremos a área máxima de um triângulo retângulo (onde um dos ângulos é ) com hipotenusa de . Podemos chamar os dois catetos desconhecidos de e , com isso temos:
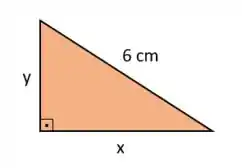
Como queremos otimizar a área, vamos escrever uma função pra ela usando a fórmula de área dos triângulos:
Passo 2
Os problemas de otimização são resolvidos com derivada, pra isso precisamos reescrever a função área como uma função de uma só variável.
Como temos um triângulo retângulo, podemos usar o teorema de Pitágoras para relacionar os valores desconhecidos e :
Vamos substituir essa relação lá na função área que escrevemos:
Passo 3
Com a função escrita só em termos de já podemos derivar, mas pra facilitar um pouco, vamos reorganizar um pouco as coisas...
Primeiro, colocando o pra dentro da raiz, que pra isso fica ao quadrado:
Vamos lembrar também que toda raiz pode ser reescrita como , temos então:
Bora derivar!
Temos uma função dentro de outra, então precisamos usar a regra da cadeia: vamos derivar a função de fora, que no caso é o expoente , e multiplicar pela derivada da função de dentro :
Já aplicamos a regra do tombo fora, agora aplicamos dentro:
Podemos descer o segundo termo trocando o sinal do expoente:
Por fim, vamos reescrever a raiz:

Eu sei, ficou uma coisa horrível... Mas eu te prometo que daqui pra frente vai tudo ficar mais simples!
Passo 4
Para encontrar os pontos críticos, nossos candidatos a máximo da função, precisamos igualar a derivada a zero.
Trazendo nosso monstrinho, temos:
O some quando passamos pro outro lado, que vai continuar sendo zero
Independente do que temos no denominador, uma fração vai ser zero quando seu numerador for zero, então pra gente só vai importar:
Viu? Muito mais simples!

Dividindo a expressão por , temos:
Prontinho, achamos o valor de um dos lados do triângulo que gera a área máxima!
Passo 5
Agora, vamos substituir na nossa relação de Pitágoras para encontrar o :
Passo 6
Finalmente, pra encontrar a área máxima substituímos os dois lados na fórmula da área:
Resolvido!