Deseja-se fabricar um recipiente cilíndrico com tampa com capacidade volumétrica de . O material destinado à lateral do recipiente custa o enquanto o material destinado ao fundo custa o . Determine a altura e o raio do recipiente de modo que o custo de fabricação seja minimizado.
Passo 1
Bom, vamos começar desenhando um recipiente cilíndrico com suas dimensões principais o raio e a altura :
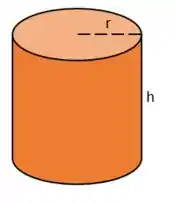
O volume do cilindro é dado pela fórmula:
Além disso, temos os custos: a parte lateral, mais escura no desenho, custa , podemos calcular essa área da seguinte forma
Enquanto a tampa e a base custam e tem sua área dada por:
Passo 2
Como queremos minimizar o custo da fabricação do recipiente, precisamos de uma função que represente esse custo. Vamos encontrar essa função pela soma das áreas multiplicadas pelos seus custos respectivos:
Obs.: Lembrando que temos base e tampa, por isso essa área entra multiplicada por 2
Simplificando a função, temos:
Passo 3
Vamos precisar da função com apenas uma variável para derivar, pra isso, vamos usar a relação do volume:
Podemos isolar o :
Agora, substituímos na função custo:
Passo 4
Agora, para encontrar os pontos críticos, vamos derivar a função custo usando a regra do peteleco:
E então, igualar a derivada a zero:
Passo 5
Finalmente, vamos calcular a altura usando a relação do volume lá do Passo 3: