Um fazendeiro tem de cerca e quer cercar um campo retangular que está na margem de um rio reto. Ele não precisa cercar o lado do terremo que ficará a margem do rio. Quais são as dimensões que ele deve usar para obter um campo com a maior área possível, podendo ser cercando com a quantidade de cerca disponível?
(a) por
(b) por
(c) por
(d) por
(e) por
Passo 1
E aí, tudo beleza?
Dá uma olhadinha no desenho aqui pra entender melhor:
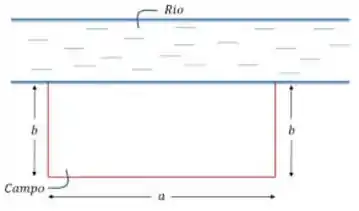
Ali temos o campo, de lados sendo que em um dos lados medindo temos a margem do rio.
Queremos saber quais sãos os valores de , nessas condições, para que o campo tenha área máxima. Vem comigo!
Passo 2
A questão nos disse que o fazendeiro tem de cerca, e a quantidade de cerca de um campo retangular é dado pelo perímetro (soma dos lados) dele.
Nesse caso vamos somar os lados com exceção do lado à margem do rio. Temos:
Como temos de cerca, nosso perímetro deverá ser:
Vamos colocar e função de :
Ok, encontramos uma relação entre os dois lados do campo. Guarda isso por enquanto!
Passo 3
A gente quer encontrar a área máxima, sendo que área do campo é dada por:
Mas, a gente achou ali em cima que:
Bora jogar isso no lugar de de na expressão da área, então?
Fazendo a distributiva:
Encontramos a expressão da área em função de 😊
Passo 4
Como queremos encontrar a maior área possível, vamos maximizar essa função:
Pra achar o ponto máximo dela, vamos encontrar onde a derivada dá zero. Vamos derivar usando a regra do Tombo:
Passo 5
Ótimo! Agora vamos ver onde essa derivada zera:
Show! Achamos o valor de que faz com que a área seja máxima!
Passo 6
Importante conferir se o ponto que encontramos é mesmo um ponto de máximo, pra isso vamos derivar a função área mais uma vez:
O teste da segunda derivada nos diz o seguinte:
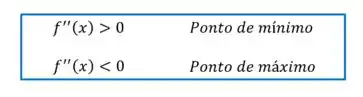
Como encontramos uma segunda derivada negativa, o ponto é um ponto de máximo!
Passo 7
Pra achar o valor da dimensão é mais fácil, porque a gente já viu que:
E como , temos:
Show de bola!
Então para que tenha área máxima, nessas condições, o campo deve medir por 😉