O produto de dois números inteiros e positivos resulta em 100. Quais são esses números, sabendo que sua soma resulta no menor valor possível?
Passo 1
Olááá! Tudo certinho?
Do enunciado, vemos que nosso objetivo aqui é encontrar dois números desconhecidos que geram o menor resultado possível quando somados.
“O menor resultado possível” é a dica que o problema nos dá pra sacar que se trata de um problema de otimização!
Nosso primeiro passo nesses problemas sempre é organizar as informações que o enunciado tá passando! Então bora lá!
Vamos chamar os dois números desconhecidos de e , então, se o produto entre os dois resulta em , podemos dizer que:
Como queremos que a soma seja o menor possível, é dela que surge a função que vamos otimizar. Escrevendo uma função pra soma, temos:
Passo 2
Como resolvemos os problemas de otimização usando derivadas, queremos que nossa função dependa de só uma variável, pra isso, vamos reescrever a expressão do produto de um jeito que possamos substituir na função soma e tirar uma das variáveis.
Olha:
Que substituindo na função, resulta em:
Agora nossa função tá prontinha pra ser derivada!
Passo 3
Podemos reescrever a função usando a propriedade onde subimos ou descemos a potência na fração trocando o sinal do expoente:
Desse jeito, fica mais fácil usar a regra do peteleco pra derivar:
Mais uma vez com a propriedade das potências, temos:
Passo 4
Para encontrar os pontos críticos da função, que são nossos candidatos a mínimo da função, vamos igualar a derivada a zero e resolver a equação:
Temos então dois candidatos: e
Passo 5
Como o enunciado especifica que os números são inteiros e positivos, podemos descartar o .
Vamos testar pra ter certeza que de fato temos um ponto de mínimo. Pra isso, precisamos da segunda derivada da função.
Derivando mais uma vez, temos:
Testando quando , temos:
O critério do teste da segunda derivada é o seguinte:
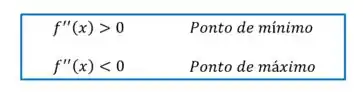
Como encontramos um resultado positivo, é um ponto de mínimo, exatamente como queríamos!
Passo 6
Pra encerrar, precisamos encontrar também o valor de , já que a questão pede os dois números!
Podemos substituir lá na primeira expressão que escrevemos pro produto igual a :
Prontinho!