Uma folha de papelão com de área será utilizada para confeccionar um cartaz. As margens livres do topo e da base do cartaz devem ter e as laterais, . Determine as dimensões da folha de modo que a área útil seja máxima.
Passo 1
Como queremos que a área útil seja máxima, temos um problema de otimização.
Vamos começar organizando os dados e montando um esquema!
É bem importante nessa questão entender bem a diferença entre a área total, que é de , e a área útil, que é o que queremos otimizar. Dá uma olhada:
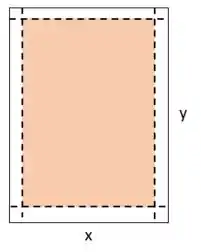
Chamei as medidas da folha de e , já que não as conhecemos.
A área total, que inclui as margens, pode ser calculada da seguinte forma:
Se considerarmos só a parte laranja, temos a área útil, que é essa parte do meio que desconsidera as margens e é calculada por:
Subtraímos duas vezes a medida da margem lateral do e duas vezes a medida da margem da base do . Essa função que precisamos otimizar!
Obs.: Pra colocar as medidas das margens na fórmula eu converti de cm para m dividindo por 100.
Passo 2
Agora precisamos reescrever a função pra derivar, pra isso, podemos usar a relação da área total:
Substituindo na função de área útil:
Vamos fazer as multiplicações:
Enfim, nossa função tá prontinha pra ser derivada!
Passo 3
Pra derivar, vamos usar a regra do peteleco, então fica mais fácil ver a função como:
Derivando, temos:
Passo 4
Para encontrar os pontos críticos, que são nossos candidatos a máximo da função, precisamos igualar a derivada a zero e resolver a equação:
Vamos multiplicar essa fração para encontrar valores inteiros e mais fáceis de seguirmos com as contas:
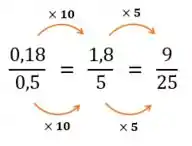
Temos, então:
Como estamos falando de medidas, não faz sentido ter valores negativos, então já podemos desconsiderar .
Temos então a área útil máxima quando !
Passo 5
Pra encerrar, vamos determinar o correspondente. Pra isso, vamos usar a relação da área total:
Prontinho!