Quando um átomo de carbono está ligado a 4 átomos, sua geometria é tetraédrica. Um exemplo é o representado abaixo.
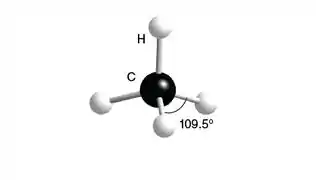
A observação de duas moléculas diferentes, o e o , apontou que a polaridade das duas moléculas é diferente. Explique qual delas é polar e qual é apolar e o motivo.
Passo 1
Como o exercício já nos deu a geometria do carbono ligado a 4 átomos, então sabemos que ele será tetraédrico. Agora é só desenhar cada uma das moléculas, e e desenhar os vetores de momento dipolo delas!
Lembrando que a ordem de eletronegatividade é:
Passo 2
Vamos dar uma olhada na molécula de . A gente pode representar ela assim:
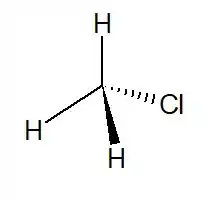
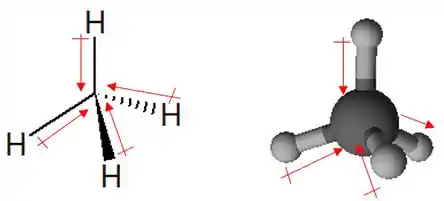
Repara que a geomatria é tetraédrica. Como o é mais eletronegativo que o , o vai ser o polo negativo dessa ligação. Já para as ligações , o carbono é o polo negativo, porque o é mais eletronegativo que o . Podemos representar assim:
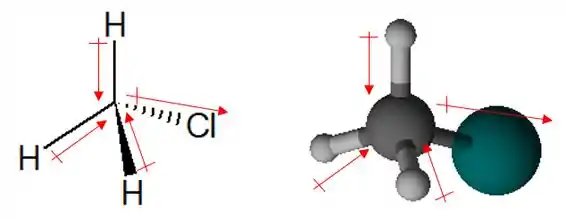
SE todos os momentos dipolos fossem iguais, devido à geometria tetragonal, eles iam se anular. Mas, acontece que o momento da ligação é maior do que o das outras ligações. Então, se a gente somar esses 4 vetores, o momento dipolo resultante vai ser um vetor apontando na direção do .
Como tem momento polar resultante, a molécula é polar.
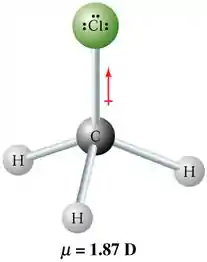
Passo 3
Chegou a hora do .
Bom, agora cada ligação é beeeem pouquinho polar, porque existe uma diferença de eletronegatividade pequena entre e . Mas devido à simetria da molécula, no fim temos uma molécula apolar.
Resposta
A molécula de é polar por ter , enquanto possui , sendo uma molécula apolar.