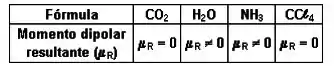
À partir da tabela a seguir, determine quais das moléculas são polares. Justifique sua resposta à partir da geometria de cada molécula.
Passo 1
Para saber qual das moléculas é polar é mole, né?
Só a gente olhar qual tem
Olhando a tabela, concluímos que as moléculas polares são: .
Para justificar a partir da geometria, precisamos analisar molécula por molécula!
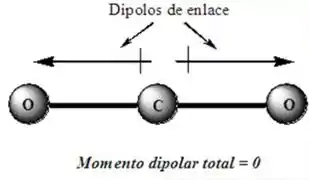
O e a são duas moléculas que tem um átomo central e dois átomos ligados a ele. Ainda assim, uma é polar e a outra apolar. Para entender a diferença, precisamos pensar no átomo central.
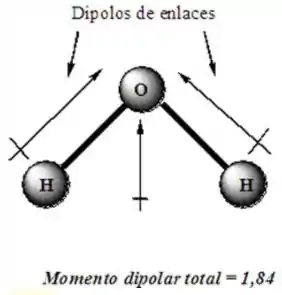
O tem geometria linear porque seu átomo central não tem um par de elétrons livres que “empurra” as ligações pra baixo! Já no caso da água, o tem dois pares de elétrons livres, o que faz com que a geometria da água seja angular 😊
Passo 2
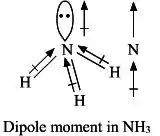
O tem uma geometria piramidal e as ligações são polares. Como consequência, os 3 momentos dipolos criados não se anulam, e o momento dipolo resultante total é diferente de zero! Assim, a molécula é polar graças à sua geometria!
Passo 3
O é um carbono rodeado de ! O é um dos átomos mais eletronegativos da tabela, e as 4 ligações vão ser polares, criando uma carga parcial negativa no e uma carga parcial positiva no C.
A geometria, porém, justifica porque a molécula é apolar:
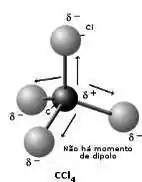
A geometria do é tetraédrica, e a soma dos vetores momento dipolo é 0.
Resposta
A água e o são polares pois tem , enquanto o são apolares pois tem
- A polaridade da água é resultado de sua geometria angular, que não anula os vetores momento dipolo quando a gente soma eles.
- A apolaridade do se explica por sua molécula ser linear (e os dois vetores momento dipolo tem a mesma intensidade e direção, mas sentidos opostos).
- A geometria piramidal do faz com que a soma dos vetores momento dipolo seja diferente de 0, e por isso a molécula é polar.
- O tem geometria tetraédrica e a soma dos seus vetores momento dipolo dão 0!