As substâncias e apresentam moléculas que possuem ligações polarizadas. Sobre as moléculas destas substâncias é correto afirmar-se que:
a) ambas são polares, pois apresentam ligações polarizadas.
b) ambas são apolares, pois apresentam geometria linear.
c) apenas o é apolar, pois apresenta geometria linear.
d) ambas são polares, pois apresentam geometria angular.
e) apenas o é apolar, pois apresenta geometria linear.
Passo 1
Para resolver esse exercício vamos tentar entender porque duas moléculas que se parecem tanto são tão diferentes!
O tem geometria angular e o geometria linear, graças ao átomo central.
Vamos por partes!
Em ambas as moléculas o átomo central está ligado a 2 átomos de oxigênio, né? Como são 3 átomos, o mais intuitivo é ajustá-los em geometria linear!
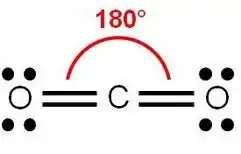
Pro essa geometria funciona bem, mas o tem um átomo central que, além de fazer duas ligações, tem um par de elétrons livres. Por isso, a geometria do vai ser angular, e não linear!
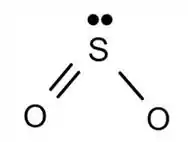
Passo 2
Agora que a gente já analisou a geometria, temos que analisar se os vetores de momento dipolo se anulam ou não!
Todas as ligações são polares, já que o é mais eletronegativo que o e que o Então, as cargas parciais vão ser sempre negativa no e positiva no outro átomo.
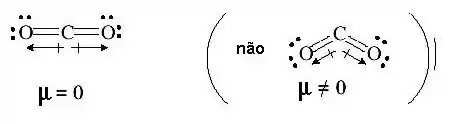
No caso do , seus dois vetores são de mesma intensidade e direção, mas estão em sentidos opostos. Por isso, o e a molécula é apolar.
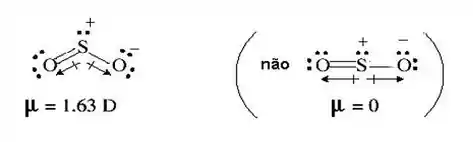
Já no caso do , os vetores de momento dipolo não somam 0, e, por isso, a molécula é polar!
Passo 3
Resumindo, o é polar pois tem uma geometria angular, que não zera seus vetores momento dipolo e o é apolar pois, apesar de suas ligações serem polares, os vetores momento dipolo se anulam, graças à sua geometria linear!
A única opção que reúne essas informações é a letra C.
Resposta
Letra C.