Exercícios Resolvidos de Pressão

Exercício 14 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17

Enunciado

PUCRIO – Física 2 2020.1 – G1– Questão 7

Considere um experimento como o dos Hemisférios de Magdeburgo onde ao invés de hemisférios temos metades de um cubo oco (de espessura desprezível) e aresta . A pressão do interior desse cubo é reduzida artificialmente até que se atinja a metade da pressão atmosférica . Qual é o valor da força que precisamos aplicar para separar as metades desse cubo (Veja a figura abaixo)?

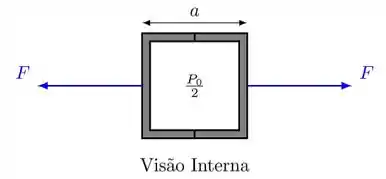
Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

A força que devemos fazer vai ser proporcional à variação de pressão (dentro e fora) do cubo:

Tranquilo até aqui?

Passo 2

A área que estamos falando é a área da face lateral do cubo, ou seja, área de um quadrado de lado :

E a variação de pressão é:

E temos que , agora é só substituir tudo na fórmula pra força:

Assim a força que será preciso é de

Beleza?

Pronto pra próxima questão? =)

Resposta

Exercícios de Livros Relacionados

As leituras dos barômetros são dadas, às vezes em polegadas de mercúrio (inHg). Determine a pressão, em polegadas de mercúrio, igual a 101 kPa.

Uma janela de escritório tem 3,4m de largura por 2,1m de altura. Como resultado da passagem de uma tempestade, a pressão do ar do lado de fora do edifício cai para 0,96a t m , mas no interior do edifí

Um peixe se mantém na mesma profundidade na água doce ajustando a quantidade de ar em ossos porosos ou em bolsas de ar para tornar sua massa específica média igual à da água. Suponha que, com as bolsa

Qual seria a altura da atmosfera se a massa específica do ar (a) fosse uniforme e (b) diminuísse linearmente até zero com a altura? Suponha que ao nível do mar a pressão do ar é 1,0a t m e a massa esp

A coluna de um barômetro de mercúrio (como o da Fig.14-5a) tem uma altura h=740,35 mm. A temperatura é - 5,0º C º , na qual a massa específica do 1nercúrio é ρ=1,3608x10 4k g / m ³ ³. A aceleração de