Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pressão

Ver Teoria
Exercício 6123457891011121314151617

Enunciado

Um recipiente em forma de cilindro está completamente cheio de um líquido. O diâmetro do cilindro é 2   cm e a altura é 10   cm .

Esse recipiente está em um plano horizontal.

A densidade do líquido é 2,0 × 10 3   kg/ m 3 .

  1. Qual é a massa do líquido?
  2. Qual é a pressão do líquido exercida no fundo do recipiente?

Considere a aceleração da gravidade g = 9,8   m/ s 2

Passo 1

Antes de começarmos, vamos dar uma olhada no que temos... Aqui temos um cilindro, em pé em um plano horizontal, esse cilindro está preenchido com um líquido, e queremos saber a massa desse líquido e a pressão que o líquido faz no fundo do recipiente.

Nosso cilindro é parecido com esse aqui ó:

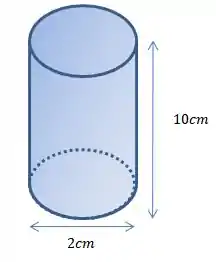
Passo 2

a)

A densidade é massa sobre volume:

ρ = m V

⇒ m = ρ × V

Sabemos a densidade:

ρ = 2 × 10 3   kg/ m 3

Agora precisamos calcular o volume pra então sabermos a massa.

Passo 3

O volume do cilindro de raio r e altura h é dado por:

V = π r 2 h

O problema nos diz o diâmetro é 2   cm . Sendo o diâmetro o dobro do raio, temos:

2 r = 2

⇒ r = 1   cm

O enunciado também diz que a altura do cilindro é h = 10   cm .

Substituindo no volume:

V = π 1   cm 2 10   cm

⇒ V = 10 π   c m 3

Passo 4

Substituindo:

m = ρ × V

⇒ m = ( 2 × 10 3   kg/ m 3 ) × 10 π   c m 3

Note que temos que igualar as unidades para eliminar o m 3 ou c m 3 .

Podemos dizer que

1   cm = 10 - 2   m

⇒ 1   cm 3 = 10 - 2   m 3

⇒ 1   c m 3 = 10 - 6   m 3

Logo:

m = ( 2 × 10 3   kg/ m 3 ) × 10 π × 10 - 6   m 3

⇒ m = 2 π × 10 - 2   kg

Aproximadamente:

m = 6,28 × 10 - 2   kg

ou

m = 62,8   g

uma vez que 1   kg = 10 3   g .

Passo 5

b)

A pressão é força sobre área:

p = F A

Então precisamos calcular essa força e essa área.

Passo 6

Calculando a força:

A força que esse líquido está exercendo no fundo do recipiente é igual à força normal entre o recipiente e o líquido, não é isso?

Como o líquido está em repouso, então a força normal é igual ao peso:

F = m g

No item anterior, calculamos a massa:

m = 2 π × 10 - 2   kg

Substituindo:

⇒ F = 2 π × 10 - 2   kg   × ( 9,8   m/ s 2 )  

⇒ F = 19,6 π × 10 - 2   N

Passo 7

Calculando a área:

A área de contato entre o líquido e o fundo do recipiente cilíndrico é a área do círculo.

Sabemos que área de um círculo de raio r é dada por:

A = π r 2

Vimos que r = 1   c m .

Convertendo para metros:

r = 1 × 10 - 2   m

Logo:

A = π × 10 - 2   m 2

⇒ A = π × 10 - 4   m 2

Passo 8

Substituindo:

p = F A

⇒ p = 19,6 π × 10 - 2   N π × 10 - 4   m 2

⇒ p = 19,6 × 10 2 N/ m 2

Como Pa =N/ m 2 :

⇒ p = 1,96 × 10 3   Pa

Resposta

  1. m = 6,28 × 10 - 2   kg
  2. p = 1,96 × 10 3   Pa

Exercícios de Livros Relacionados

As leituras dos barômetros são dadas, às vezes em polegadas de mercúrio (inHg). Determine a pressão, em polegadas de mercúrio, igual a 101 kPa.
Uma janela de escritório tem 3,4m de largura por 2,1m de altura. Como resultado da passagem de uma tempestade, a pressão do ar do lado de fora do edifício cai para 0,96a t m , mas no interior do edifí
Um peixe se mantém na mesma profundidade na água doce ajustando a quantidade de ar em ossos porosos ou em bolsas de ar para tornar sua massa específica média igual à da água. Suponha que, com as bolsa
Qual seria a altura da atmosfera se a massa específica do ar (a) fosse uniforme e (b) diminuísse linearmente até zero com a altura? Suponha que ao nível do mar a pressão do ar é 1,0a t m e a massa esp
A coluna de um barômetro de mercúrio (como o da Fig.14-5a) tem uma altura h=740,35 mm. A temperatura é - 5,0º C º , na qual a massa específica do 1nercúrio é ρ=1,3608x10 4k g / m ³ ³. A aceleração de