Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Uma corda muito longa é mantida tensa e, por ela, se propaga uma onda transversal, cujos deslocamentos verticais são dados por:
onde , e são constantes positivas. Considere que, no equilíbrio, a corda se encontra na horizontal ao longo do eixo . A figura que representa corretamente a configuração da corda no instante e as velocidades dos pontos , , e da corda é:
a)
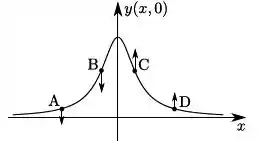
b)
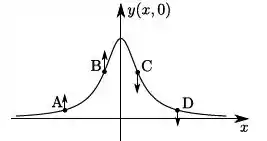
c)
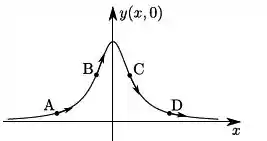
d)
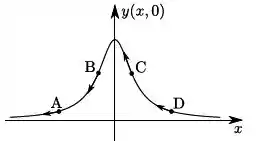
e)
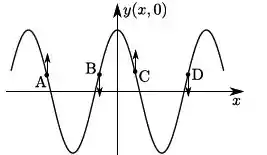
f)
Passo 1
As velocidades da figura são referentes às velocidades transversais dos pontos. Então, o que devemos fazer? Bora calcular uma expressão pra velocidade transversal desse pulso, através da derivada:
E vamos aplicar à equação:
Passo 2
Aqui você vai precisar lembrar da regra da cadeia. Simbora:
Notou? Aplicamos a regra da cadeia ali.
Passo 3
Agora que temos uma expressão pra velocidade, podemos avaliar o sinal dela para cada ( afinal de contas, o gráfico varia em função de .
Vamos analisar a função para um tempo fixo e determinar as regiões onde ela é positiva, vetor velocidade apontando para cima, e negativa, vetor velocidade apontando para baixo.
Passo 4
Para a região negativa, teremos:
Como o denominador é sempre positivo, podemos dizer que:
E como as constantes e são positivas:
Como estamos analisando em
Ou seja, a velocidade transversal vai ser negativa quando for negativo.
O que nos leva a perceber que o contrário também é facilmente descoberto: A velocidade transversal vai ser positiva quando o for positivo.
Ou seja:
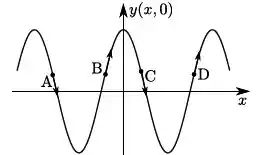
A resposta correta é:
a)
Resposta
a)