Um pulso, se movendo em uma corda esticada com tensão , é descrita pela função de onda:
- Faça um gráfico de como função de .
- Qual o valor da magnitude da velocidade de propagação do pulso e sua direção?
- Calcule a velocidade transversal de um dado ponto da corda num instante
Passo 1
a)
Bom, aqui nós vamos ter que primeiro fazer uma manipulação de variáveis pra encontrar a nossa função :
Isolando no denominador e no numerador:
Se a gente fizer , vamos obter o valor 1. Se a gente fizer tender ao infinito, a função tende a zero, assim como se a gente fizer tender a menos infinito.
Logo, o gráfico da função fica:
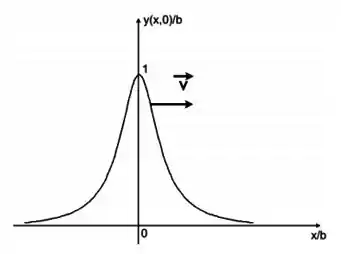
Passo 2
b)
Se a gente considerar um observador se movendo na mesma direção do pulso e com a mesma velocidade que ele, esse observador o veria parado, certo? Ou seja, sem dependência temporal.
Se a gente reescrever a função do pulso excluindo a parte que funciona como uma função do tempo (no caso , podemos escrever:
Legal...Mas e daí?
Bom, agora a gente tem que pensar em como fizemos essa transformada. Se a gente tomar:
E depois substituir na equação original:
Que é a equação do pulso parado.
Só que a equação é justamente a equação de um móvel se movendo com velocidade na direção positiva do eixo
Logo, como estávamos supondo que esse observador estava se deslocando na mesma velocidade que o pulso, a velocidade do pulso será:
Passo 3
c)
Bom, pra se calcular a velocidade transversal de um ponto na corda num instante qualquer, a gente precisa derivar parcialmente a função em relação a . Ou seja:
Isso acontece porque a gente ‘congela’ um qualquer e apenas varia o tempo dele, ou seja, o ponto passa a se mover pra cima e pra baixo, apenas transversalmente.