Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra do Produto e do Quociente

Ver Teoria
Exercício 21345678910

Enunciado

Considere a função f x = x 3 + 2 x 2 - 3 x 2 + 3 . Indique qual a opção abaixo para d f d x .

(a) d f d x = x 4 + 9 x 2 - 18 x x 4 + 6 x 2 + 9

(b) d f d x = x 4 + 9 x 2 + 18 x x 4 + 6 x 2 - 9

(c) d f d x = x 4 - 9 x 2 + 18 x x 4 + 6 x 2 + 9

(d) d f d x = x 4 + 9 x 2 + 18 x x 4 + 6 x 2 + 9

(e) d f d x = x 4 + 9 x 2 + 18 x x 4 - 6 x 2 + 9

Passo 1

Opa! Tudo joia? Olha só, a gente quer a derivada dessa função aqui:

f x = x 3 + 2 x 2 - 3 x 2 + 3

Bom, aqui a gente tem um quociente de polinômios, certo? A gente usa então a Regra do Quociente, que é assim:

g h ' = g ' ⋅ h - g ⋅ h ' h 2

E no nosso caso:

g = x 3 + 2 x 2 - 3

h = x 2 + 3

Beleza? Vamos continuar...

Passo 2

A gente precisa das derivadas dessa g   e   h ali. Vamos ver isso então:

g = x 3 + 2 x 2 - 3

Pra derivar essa, podemos usar a regra do Tombo nesses expoentes aí, tá lembrado? Essa aqui ó:

x n ' = n ⋅ x n - 1

Aplicando isso em g :

g ' = 3 ⋅ x 3 - 1 + 2 ⋅ 2 x 2 - 1 - 0

(derivada de constante é sempre zero😉)

g ' = 3 x 2 + 4 x

Passo 3

Show! Vamos fazer a mesma coisa com h :

h = x 2 + 3

h ' = 2 x 2 - 1 + 0

h ' = 2 x

Beleza! Agora que temos as derivadas de cima e de baixo, podemos montar nossa regra do quociente!

Passo 4

Substituindo tudo isso na fórmula:

g h ' = g ' ⋅ h - g ⋅ h ' h 2

f ' x = 3 x 2 + 4 x x 2 + 3 - x 3 + 2 x 2 - 3 ( 2 x ) x 2 + 3 2

Vamos aplicar a distributiva nessas multiplicações ali da parte de cima: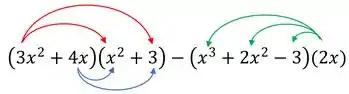

Então:

f ' x = 3 x 4 + 9 x 2 + 4 x 3 + 9 x 2 + 12 x - 2 x 4 - 4 x 3 + 6 x x 2 + 3 2

Juntando os termos semelhantes:

f ' x = x 4 + 9 x 2 + 18 x ( x + 3 ) 2

Essa é a derivada! Pra chegar na resposta de alguma daquelas alternativas,vamos ter que expantir aquele parênteses ali do denominador...

Passo 5

Vamos lá, você lembra o que é isso aqui?

x + 3 2

É um produto notável dessa forma aqui:

a + b 2 = a 2 + 2 a b + b 2

Aplicando naquele caso aliesse produto notável ao nosso caso:

x + 3 2 = x 2 + 2 ⋅ x ⋅ 3 + 3 2

= x 2 + 6 x + 9

Beleza! Expandimos os parênteses, vamos substituir na derivada agora!

Passo 6

Voltando aqui:

f ' x = x 4 + 9 x 2 + 18 x ( x + 3 ) 2

Substituímos:

f ' x = x 4 + 9 x 2 + 18 x x 2 + 6 x + 9

E assim chegamos na resposta da letra D 😊

Resposta

(d) d f d x = x 4 + 9 x 2 + 18 x x 4 + 6 x 2 + 9