Derive a função
Passo 1
Olá! Bora resolver mais essa?
Queremos derivar essa função e ela é formada por uma multiplicação. Daí a gente já sabe que vamos ter que usar a regra do Produto, certo?
Só pra relembrar, a regra do Produto é assim:
Sendo que o “ “ representa a derivada da função😉
Passo 2
Vamos definir agora quem é e quem é . A ordem não importa, mas vamos chamar assim:
Então temos:
Show! Agora vamos derivar cada uma dessas, porque na regra do produto precisaremos de e ...
Passo 3
Derivando ...
Temos que é uma soma entre uma potência e uma exponencial. A gente pode derivar cada termo e manter a soma. Potência e exponencial a gente já aprendeu a derivar, lembra? Vai ficar assim:
Como qualquer coisa elevada a zero dá um:
Beleza, já derivamos !
Passo 4
Vamos derivar agora. Veja que, podemos escrever como usando essa regrinha aqui:
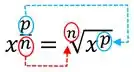
Com isso, podemos escrever assim:
Agora derivamos. Derivada de constante é zero e a a gente deriva usando a regra da Potência (ou regra do Tombo)...
Essa subtração de fração no expoente a gente vai ter que colocar com frações de denominadores iguais, assim transformamos o em :
E então nossa derivada é:
Que a gente ainda pode jogar em forma de raiz e descer pro denominador (por causa do expoente negativo, a gente inverte):
Ufaa! Derivamos ! Agora vamos montar nossa Regra do Produto...
Passo 5
Voltando pra nossa derivada principal, vamos montar a regra do Produto, sendo:
Substituindo todo mundo:
E aí a gente pode fazer essas multiplicações, usando a distributiva (multiplica cada termo de um parênteses por cada termo do outro), pra deixar a derivada mais arrumadinha...
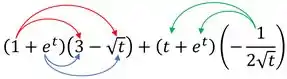
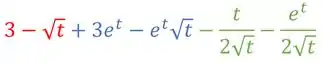
E pronto! Essa é a nossa derivada😉