Seja
A derivada calculada para corresponde a:
(a)
(b)
(c)
(d)
(e)
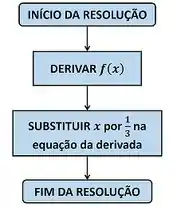
Passo 1
Opa, galera, prestem atenção no enunciado, porque dessa vez não precisamos apenas derivar . Precisamos também substituir por depois que a gente derivar ! E o resultado dessa substituição é que será a resposta da questão!
Esse é mais um exercício que o aparece em cima e embaixo da divisão! Sabemos que nesses exercícios, antes de começar a derivar uma função com divisão, temos que dar nomes para cada termo. Assim a gente se organiza melhor para quando for derivar.
Vamos chamar o termo de cima da fração de e o termo debaixo de .
Usando e podemos reescrever .
Mas como dar nomes ao termo de uma divisão pode organizar a resolução da questão?
Passo 2
Para derivar uma divisão, usamos uma regra chamada de regra do quociente.
A gente deu nome a cada parte da divisão no passo 1 para escrever a regra do quociente de um jeito mais fácil agora. Abaixo a gente pode ver a cara dessa regra.
Lembre-se que usamos o símbolo (chamado de apóstrofo) para representar as derivadas! Ou seja, é a derivada de , é a derivada de e é a derivada de !
Como e estão presentes na regra do quociente, precisamos calcular as derivadas de e para achar
Passo 3
Nesse passo, vamos calcular quanto vale a derivada de .
.Mas não precisamos derivar e ao mesmo tempo. Podemos calcular a derivada de cada um e só depois somar as duas para achar .
O e um número constante. Como a derivada de constantes vale zero, a derivada de um é nula!
Já para derivar usamos a regra do peteleco. Nessa regra, o expoente de leva um peteleco e cai na frente de . Além disso, o expoente deixa pra trás ele mesmo menos 1.
E qual é o expoente de para a gente aplicar essa regra?
é igual a . Isso quer dizer que seu expoente vale .
Logo, sua derivada é:
Somando as duas derivadas achamos quanto vale .
Passo 4
Nesse passo, temos que calcular quanto vale a derivada de .
, bem parecido com o de cima, né! Podemos, aqui também, calcular a derivada de e separadamente e só depois juntar as duas para achar .
No entanto, nós já calculamos quanto vale a derivada de e no passo anterior.
Juntando as duas derivadas achamos quanto vale .
Passo 5
Já temos tudo pra substituir na regra do quociente:
Agora vamos substituirpara calcular !
Ajustando as multiplicações:
Esse menos na frente do segundo parênteses altera o sinal de todo mundo que está lá dentro Assim, tirando os parênteses teremos:
Podemos cancelar o negativo com o positivo ficando com:
E já tá bonito. Mas calma, porque ainda não acabamos! Ainda temos que substituir o por ! Lembra?
Passo 6
Nesse passo vamos valcular o valor da derivada para . Para fazer isso, vamos substituir por na equação de que encontramos no passo anterior.
Para fazer a conta de , temos que colocar no mesmo denominador que .
Fazemos isso escrevendo o como . Podemos fazer isso porque . Assim:
Agora que os denominadores são iguais, nos resolvemos em cima e repetimos embaixo:
Substituindo esse valor na fórmula, achamos:
Aqui nós temos que elevar ao quadrado! Você se lembra como podemos fazer isso?
Para elevar uma fração ao quadrado, elevamos a parte de cima e a parte debaixo ao quadrado separadamente.
Substituindo isso na equação:
Útima coisa! Prometo!
Chegamos da divisão de por . Para fazer essa conta, mantemos o igual e multiplicamos ele pelo inverso de que vale .
E esse é o resultado final. Ou seja, agora é só marcar a letra (c) e comemorar!
Resposta
Letra (c).