Exercícios Resolvidos de Retrato de Fase e Classificação de Ponto Crítico – Caso Não Linear
Ver TeoriaEnunciado
Retratos de Fase
Considere o problema abaixo que representa o comportamento de duas espécies (com densidades populacionais e ) competindo por suprimentos comuns.
- Determine as singularidades e classifique-as.
- Esboçe as trajetórias do retrato de fase no primeiro quadrante.
- Para quais condições iniciais existe uma configuração de equilíbrio na qual nenhuma espécie desaparece, e qual é esta configuração?
Passo 1
Resolvendo a letra a)
Pra encontrar as singularidades, devemos igualar as derivadas e a zero! E encontrar valores de e que satisfaçam o sistema. Vamos lá:
Com :
Com
Então, as singularidades são: . E agora devemos classificá-las!!
Passo 2
Pra classificá-las, devemos construir a matriz Jacobiana, que carrega as derivadas das expressões das populações em relação a e . Veja só:
E pra esse caso, a matriz será:
E utilizamos o critério de traço e determinante da matriz em cada singularidade pra classifica-las!
Pra
Portanto:
Então, é repulsor!
Pra :
Portanto:
Então, é sela!
Pra :
Portanto:
Então, é sela!
Pra :
Portanto:
Então, é atrator!
Passo 3
Resolvendo a letra b)
O retrato de fase será mais ou menos assim:
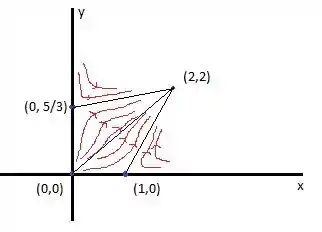
Passo 4
Resolvendo a letra c)
Como é atrator, qualquer condição inicial fora dos eixos irá convergir pra solução de equilíbrio . A única solução que não há extinção é a solução com dados iniciais ! Condições iniciais sobre os eixos resultam na extinção de pelo menos uma das duas espécies.
Resposta
a)