Exercícios Resolvidos de Retrato de Fase e Classificação de Ponto Crítico – Caso Não Linear
Ver TeoriaEnunciado
Sistema de EDO de Dimensão 2 - Retrato de Fase
Considere o problema abaixo que representa o comportamento de duas espécies(com densidades populacionais e) competindo por suprimentos comuns.
- Determine as singularidades e classifique-as.
- Esboce as trajetórias em uma vizinhança de cada singularidade no primeiro quadrante.
- Para quais condições iniciais existe uma configuração de equilíbrio na qual nenhuma espécie desaparece, e qual é esta configuração?
Passo 1
Resolvendo a letra a)
Pra encontrar singularidades, devemos fazer:
E resolvendo o sistema:
Encontraremos os pontos:
Passo 2
Pra classificar as singularidades, devemos construir a matriz jacobiana e avalia-la em cada singularidade.
Pra :
Teremos que:
E portanto é uma fonte, ou seja, é repulsor!
Pra :
Teremos que:
E portanto é uma sela hiperbólica!
Pra :
Teremos que:
E portanto é um poço, ou seja, é atrator!
Passo 3
Resolvendo a letra b)
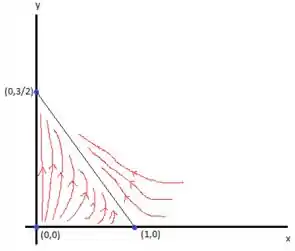
Passo 4
Resolvendo a letra c)
Visto que as singularidades ficam sobre os eixos, concluímos que não há nenhuma configuração de equilíbrio na qual as duas espécies sobrevivam!
Resposta
Exercícios de Livros Relacionados
Considere o elipsoide.Determine uma condição suficiente sobre c para que toda trajetória cruzando V(x, y, z) = c esteja orientada para dentro. Calcule a condição encontrada no caso em que σ = 10, b =
Considere o elipsoide.Calcule dV/dt ao longo das trajetórias das equações de Lorenz (1).
Desenhe um campo de direções e descreva como as soluções parecem se comportar.
Encontre os pontos críticos.
Considere o sistemaem que σ0. Note que esse sistema é uma modificação do sistema (2) no Exemplo 1.Determine o tipo e as propriedades de estabilidade de cada ponto crítico. Encontre o valor σ1