Exercícios Resolvidos de Retrato de Fase e Classificação de Ponto Crítico – Caso Não Linear
Ver TeoriaEnunciado
Sistema de EDO de Dimensão 2 - Retrato de Fase
Considere o seguinte modelo que pode ser interpretado como a interação entre duas espécies.
- Ache as singularidades do sistema e classifique-as
- Esboce o retato de fase do sistema
- Quais são as trajetórias que tem limite quando tende a e que configurações representam no modelo?
Passo 1
Vamos começar achando os pontos críticos fazendo e
Podemos reescrever essas duas equações como
Pela primeira equação vamos ter
Substituindo o valor de na segunda equação vamos ter
Então um ponto seria
O outro ponto seria
E o outro ponto seria
Passo 2
Agora que temos os pontos vamos fazer a análise da matriz jacobiana, mas lembra como ela vai ficar?
Vamos ter
A matriz jacobiana vai ser
Passo 3
Vamos começar analisando o ponto , o jacobiano nesse ponto vai ficar
Vamos achar os autovalores desse cara
Resolvendo isso vamos ter
Vamos ter dois autovalores reais, Com sinais trocados, neste caso o ponto crítico é chamado de ponto de sela.
Passo 4
Vamos agora para o ponto , o jacobiano nesse ponto vai ficar
Vamos achar os autovalores desse cara
Como temos o negativo isso é um número complexo
Vamos ter dois autovalores complexos sem a parte real, ou seja complexos puros, então esse ponto crítico vai ser um Centro.
Passo 5
O retrato de fase do ponto crítico que é um centro é de boa de fazer, basta fazer alguns círculos, lembrando que esse ponto é , o retrato de fase é algo parecido com isso
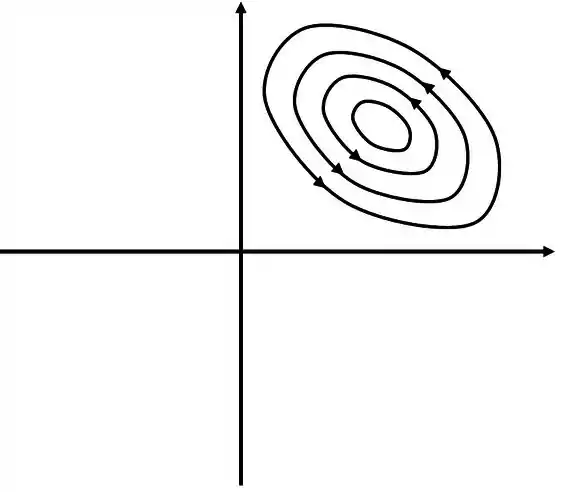
Esse desenho está descentralizado porque o centro é o ponto da singularidade é não é a origem, é
Passo 6
Para o outro como depois ele quer a analise vamos achar os autovetores desses caras, vai ser tranquilo nesse caso. Temos que resolver a seguinte equação para cada autovalor
Primeiro para , vamos ter sendo
Dessa forma devemos ter sendo . O autovetor vai ficar
Podemos tirar esse
Vamos ao outro autovetor, para
Dessa forma devemos ter sendo . O autovetor vai ficar
Podemos tirar esse
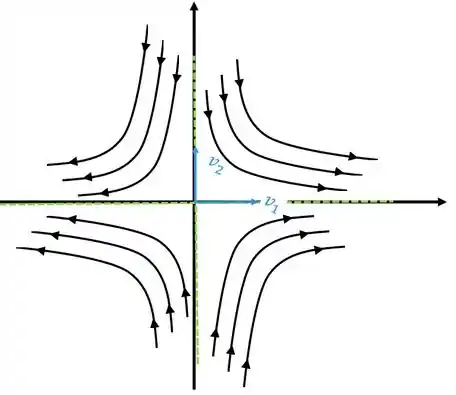
Então aqueles eixos do retrato de fase são os próprios eixos e .
Passo 7
O tratado de fase de vai ficar
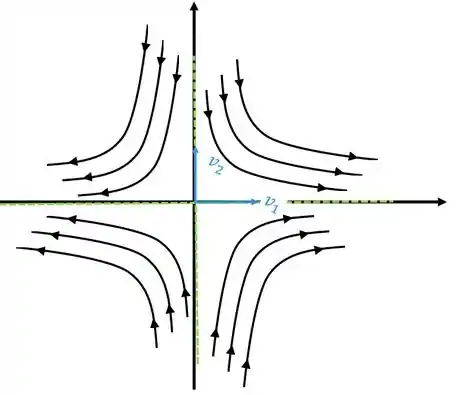
Passo 8
As trajetórias que tem limite são aquelas linhas verdes, que são as soluções que contém o ponto crítico. Nesses casos é uma linha que começa no infinito de e vai até a singularidade, podemos perceber que nesse caso, e vamos ter o valor de tendendo a .
Sempre que tiver uma parada dessa vamos procurar as linhas que contém a singularidade, que é o ponto crítico.
Resposta
Os pontos críticos são , que é um ponto de sela, e o ponto que é um ponto de centro.
Retrato de fase de
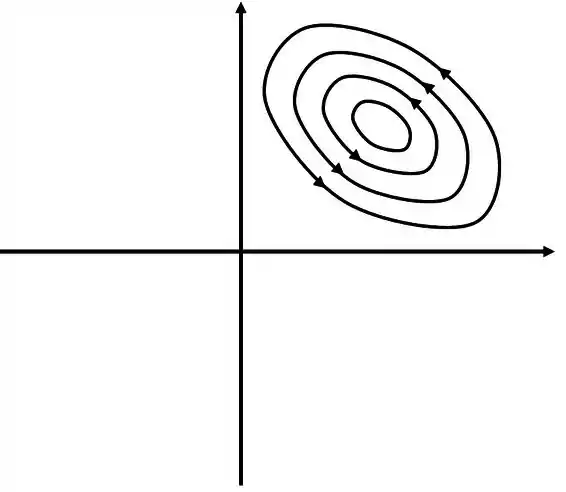
Retrato de fase do ponto de centro.
