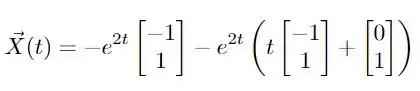UFMG, Sem Campus, Equações Diferenciais A, P3 - 2015.1, Questão 4
Resolva o sistema
Passo 1
Oiie, tudo certinho?
O enunciado nos dá o seguinte sistema de equações diferenciais
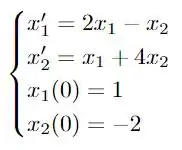
e precisamos encontrar uma solução! Existe todo um processo para encontrar a solução deste problema usando autovalores e autovetores de uma matriz relacionada, o primeiro passo então! Será escrever o nosso sistema de equações no formato de uma matriz! Vamos lá!
Passo 2
Em forma de matrizes e vetores, temos que
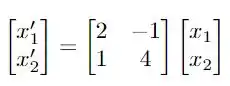
Sistemas de equações lineares tem solução da seguinte forma
nós temos que e são os autovalores relacionados aos autovetores e . Eles obedecem a seguinte relação
em que os autovalores são obtidos através do polinômio característico obtido como
em que a matriz é dada por
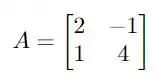
Vamos tentar resolver isso agora! Vem comigo!
Passo 3
Primeiro, temos que escrever a matriz , ela é da forma
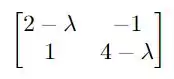
o determinante desta matriz é tal que
Juntando os termos e igualando a zero, temos que
Aplicando Bhaskara temos que
Portanto, temos dois autovalores repetidos da forma
Vamos construir agora nossos autovetores! Saca só!
Passo 4
Usando a relação para os autovetores com , temos que
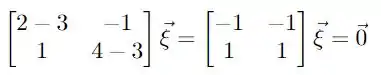
Usando que é um vetor com duas componentes, podemos fazer o produto de matrizes para obter
Ou seja, nosso vetor tem que obedecer a relação , ou seja, podemos usar o seguinte autovetor
Em geral usamos o outro autovalor para obter outro autovetor, mas nossos autovalores são exatamente iguais, portanto, não é possível obter um segundo autovetor ortogonal ao que encontramos. Vamos ter que utilizar uma outra relação! Saca só!
Passo 5
A relação usual para se obter outro vetor ortogonal é tal que
utilizando o vetor que obtivemos no passo anterior, e a matriz que construímos, temos que resolver
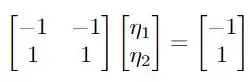
As equações resultantes são tal que
e, também
Como esperado, as duas equações são as mesmas, e portanto, temos que o vetor desejado irá obedecer . Se escolhermos que , iremos obter que
Vamos escrever finalmente a nossa solução! Para o caso de autovalores repetidos, a solução para o sistema de equações diferenciais com autovalores é repetidos é tal que
ou seja, nossa solução é
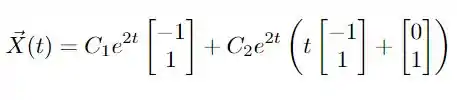
Agora é só aplicar as condições iniciais! Então bora lá!
Passo 6
Em , temos que e , portanto, a nossa solução obedece a seguinte relação
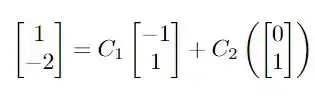
O que é equivalente ao sistema de equações lineares da forma
e, também
como temos que , temos que também! E assim, a solução se torna
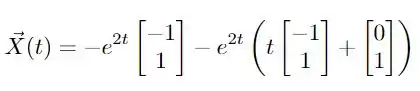
A questão é isso! Te vejo na próxima! Tchau Tchau!
Resposta
