Consideremos o seguinte sistema de equações lineares, ache as soluções:
Passo 1
Animados para mais uma solução bem legal ?! Entãao boora !!
Nós vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
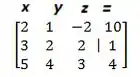
Só colocamos as equações como matriz certo?
Para achar o pivô na primeira coluna podemos dividir tudo por 2, certo?
Então:
Agora precisamos zerar estes números abaixo do nosso pivô na primeira coluna, e aí ? Como faremos?
Que tal usarmos:
Então:
Agora, temos que achar o pivô para a segunda coluna, e para isso podemos transformar em 1 multiplicando tudo da linha 2 por -2:
Então:
Para zerar o termo na última linha podemos fazer:
Então:
Quando chegamos nesse ponto nós já facilitamos muito as coisas, certo?
Passo 2
Agora vamos transformá-la novamente em equações lineares !!
Não se esqueçam que cada linha correspondem a uma equação, cada coluna representa um companheiro para o x, y, z e a igualdade:
Da terceira equação nós podemos achar o z, basta passar o 7 para o outro lado dividindo:
Na segunda equação nós substituímos o z:
Passando o termo 30 para o outro lado da igualdade com sinal contrário:
Na primeira equação nós podemos substituir o y e o z:
O termo 4 passa para o outro lado da igualdade com o sinal oposto:
E assim nós finalizamos mais umaa !!
Legal, não é?