Consideremos o seguinte sistema de equações lineares, ache as soluções:
Passo 1
Boom galerinha, o escalonamento é algo bem importante, não é?
Isso porque nós podemos escrever sistemas lineares na forma de uma matriz, e ao escalonar nós conseguimos achar a solução do problema de forma mais fácil do que substituindo um no outro, como fazíamos lá no ensino médio !!
Então vamos montar uma matriz onde cada linha corresponde a uma equação linear e cada coluna representa o companheiro do assim como o resultado!!
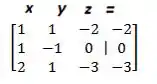
Só colocamos as equações como matriz certo?
A primeira coluna já tem o seu pivô!! Então vamos zerar a segunda e a terceira linha, certo?
Para fazer isso nós podemos usar a primeira linha e manipular a segunda e terceira juntinho! Vamos pensar aqui em uma operação:
Agora vamos só fazer as continhas:
Para encontrar o pivô da segunda nós precisamos transformar este 2 aí em 1, por isso nós podemos dividir toda essa segunda linha por dois, ok?
Então:
E para zerar o termo abaixo desse pivô? O que faremos?
Podemos subtrair a linha 3 de 2, certo?
Então:
Passo 2
A terceira linha é toda nula, ou seja, não temos pivô para a variável z, e o que isso nos diz?
Nos diz que z é uma variável livre, ou seja, pertence aos números reais e pode ter qualquer valor, então nós vamos colocar as outras variáveis em função dela !!
Bom, a nossa matriz já tem os pivôs, então só nos resta transformá-la novamente em equações lineares !!
Da primeira linha:
Na segunda coluna nós podemos isolar o y passando o termo z para o outro lado da igualdade com sinal contrário:
Na primeira equação nós podemos substituir o y pelo que acabamos de achar:
Somando os termos contendo o z:
Os termos 1 e z passam para o outro lado da igualdade com o sinal oposto:
E assim nós acabamos de achar a solução:
Então, para cada valor de z diferente, teremos um ponto diferente !!
O que acharam desta?