Consideremos o seguinte sistema de equações lineares dadas como matriz, ache as soluções:
Passo 1
Faaaala galerinhaa !! Prontos para mais uma ?!
Que estranho... o exercício dá uma matriz e nos pede para resolver um sistema linear... Cadê o sistema linear?!
Calma!
Essa matriz que tá aparecendo é chamada de matriz ampliada do sistema linear. Cada linha representa uma equação do sistema, e a gente pode pensar nas colunas assim: A primeira coluna contém os números que vão multiplicar o , na segunda coluna a gente tem os números que vão multiplicar o e na última coluna, a gente tem os resultados:
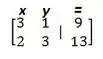
Essa matriz é a mesma coisa que esse sistema aqui ó:
Boom galerinha, o escalonamento é algo bem importante, não é?
Isso porque nós podemos escrever sistemas lineares na forma de uma matriz, e ao escalonar nós conseguimos achar a solução do problema de forma mais fácil do que substituindo um no outro, como fazíamos lá no ensino médio !!
Vamos começar achando o pivô para a primeria coluna, certo?
E como faremos para fazer aparecer o 1 no lugar do 3?
Podemos fazer:
Então:
Agora nós vamos precisar zerar estes termos abaixo do pivô, ok? Isso vai facilitar na hora de resolvermos nosso sisteminha!
Para isso podemos fazer:
Então:
Para resolver essa operação com frações na segunda linha a gente faz:
Então nossa matriz fica dessa forma aqui:
Bom, nós podíamos seguir a achar o pivô para a segunda coluna, mas quando chegamos nesse ponto nós já achamos uma incógnita em função do resultado, certo?
Como assim?
Bom, a segunda linha representa a segunda equação, a primeira coluna o x, a segunda o y e a terceira a igualdade !! Se é assim, na segunda linha nós temos o x nulo, então o y está em função da igualdade!!
Passo 2
Podemos transformar esta matriz novamente em sistemas lineares
Na segunda equação nós podemos isolar o y, certo?
Vamos passar quem tá multiplicando o para o outro lado da igualdade. Cuidado que quando a gente faz isso, quem multiplica passa a dividir e quem dividi passa a multiplicar:
Na primeira equação nós podemos substituir o y pelo que acabamos de achar:
Agora o 1 vai lá para o outro lado da igualdade com o sinal oposto:
Olha que massa !!
Acabamos de achar a solução:
Bora continuar ?!