Consideremos o seguinte sistema de equações lineares dadas como matriz, ache as soluções:
Passo 1
Mais uma beem legal !! Animados para seguir?
Já vimos que cada linha representa uma equação, e cada coluna um companheiro para as letrinhas assim como o resultado:
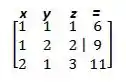
A primeira linha já veio com o pivô para facilitar a nossa vida, certo?
Então vamos começar pensando em como zerar os números abaixo dele, 1 e 2, ok?
Para isso nós podemos fazer as seguintes operações:
Então:
E com isso nós já achamos o pivô para a segunda coluna, certo?
Então vamos tentar zerar esse -1 que está em baixo dele, certinho?
Vamos fazer isso somando a linha 3 com a 2, assim dá certo, concordam?
Então:
Nós podíamos manipular mais, mas só até esse ponto já nos facilita, e muito, a vida, não é?
Passo 2
Se nesse ponto ela já nos ajuda, então só nos resta transformá-la em equações lineares !!
Lembrando que cada linha é uma equação linear, a primeira coluna é o par do x, a segunda do y, a terceira do z e última a igualdade:
Da terceira linha nós conseguimos achar o z:
O 2 que está do ladinho de z passa para o outro lado dividindo, certo?
Na segunda coluna nós podemos achar o y, basta substituirmos o z:
O 1 vai passa para o outro lado da igualdade com o sinal oposto, e deixar o y sozinho, só assim pra gente conseguir achá-lo:
Na primeira equações nós podemos substituir o y pelo que acabamos de achar:
E agora é a vez do 3 passar com sinal oposto para o outro lado:
E assim nós achamos a solução para este sistemaa !!
Gostaram?!