Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Tensão Cisalhante Média e Esforço Cortante

Ver Teoria
Exercício 41235678910

Enunciado

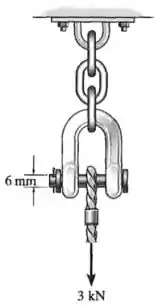
O arganéu da âncora suporta uma força de cabo de 3   k N . Se o pino tiver diâmetro de 6   m m , determine a tensão média de cisalhamento no pino.

Passo 1

Nesse exercício, o pino está sob a situação que chamamos de cisalhamento duplo.

Ele transmite entre as peças uma força total F = 3   k N , mas a força cortante interna V máxima a qual ele está submetido é metade dessa força:

V = F / 2 = 1,5   k N

Com esse valor de V e com a área A da seção transversal do pino (calculada a partir do diâmetro d = 6   m m ), conseguimos encontrar a tensão cisalhante média no pino:

τ = V A

E assim o exercício está resolvido.

Se for preciso, Diagramas de Corpo Livre do pino podem ser feitos para provar que V = F / 2 :

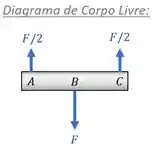
Do ponto A até o ponto B, temos F/2 para cima. Do ponto B até o ponto C, temos F/2 para baixo.

Passo 2

Vamos começar calculando a área A da seção transversal do pino.

É uma área circular e nos foi fornecido o diâmetro dela, então usamos a equação:

A = π d 2 4

Substituindo d = 6   m m :

A = π 6   m m 2 4

⇓

A = 28,3   m m 2

Passo 3

Como já temos V = 1,5   k N e A = 28,3   m m 2 , podemos aplicar a fórmula da tensão cisalhante média:

τ = V A = 1,5   k N 28,3   m m 2

Para ter resultados em M P a = N / m m 2 , reescrevemos a força de 1,5   k N como 1500   N :

τ = 1500 N   28,3   m m 2 = 1500 28,3   M P a

Resposta

τ = 53,0   M P a

Exercícios de Livros Relacionados

Resolva o problema 1.61 para o pino B , qual está sujeito a cisalhamento duplo e tem 5 m m de diâmetro.
Um tubo de aço de 400 mm de diâmetro externo é fabricado a partir de uma chapa de aço com 10 mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 20° com um plano perpendicular ao ei
Determine a maior carga P que pode ser aplicada em A quando Ø=60 °, sabendo que a tensão de cisalhamento média no pino de 10 mm de diâmetro em B e não deve exceder 120 MPa e que a tensão média de cont
Dois elementos de madeira de seção transversal retangular uniforme são unidos por uma emenda colada como mostra a figura. Sabendo que a tensão de cisalhamento máxima admissível na emenda colada é de 6
A carga P de 6227 N é suportada por dois elementos de madeira de seção transversal uniforme unidos pela emenda colada mostrada na figura. Determine as tensões normais e de cisalhamento na emenda colad