Um parafuso para finalidades especiais de diâmetro passa através de um furo em uma placa de aço (veja a figura). A cabeça hexagonal do parafuso está direcionada contra a placa de aço. O raio do círculo circunscrito pelo hexágono é (o que significa que cada lado do hexágono tem comprimento ). A espessura da cabeça do parafuso é de e a força de tração no parafuso é de .
Determine a tensão de cisalhamento média na cabeça do parafuso.
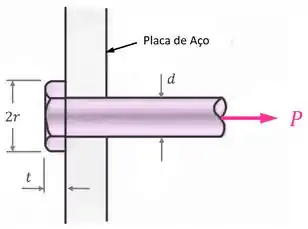
Passo 1
O exercício quer saber a tensão de cisalhamento média na cabeça do parafuso:
Precisamos então identificar:
- qual à a força cisalhante interna na cabeça do parafuso;
- e qual é a área da seção resistente à essa força.
Para tanto, vamos visualizar um diagrama de corpo livre da cabeça de um parafuso que está sendo tracionado por uma força :
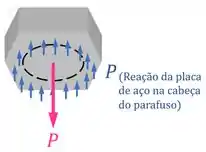
O que está acontecendo: a placa de aço exerce uma força em volta de toda a cabeça do parafuso, de intensidade total , para o segurar o parafuso no seu lugar.
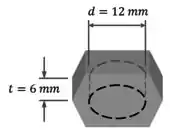
A linha tracejada indica uma superfície cilíndrica de diâmetro e altura que é a seção resistente ao cisalhamento:
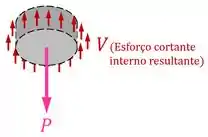
A figura abaixo mostra os esforços internos nessa seção:
Na prática, você não precisa fazer todos esses desenhos. O que precisamos é saber interpretar o exercício para chegar às conclusões que:
- Para garantir o equilíbrio desse pedaço da cabeça do parafuso mostrado na última imagem, deve ser igual à ;
- A área da seção resistente é como a área da face lateral de um cilindro de diâmetro e altura .
A dimensão fornecida pelo enunciado para os lados da cabeça hexagonal do parafuso não será utilizada pela gente nesse exercício: ela não é necessária para encontrar , ou .
Passo 2
Vamos começar então calculando a área .
Pensa aí... A área da face lateral de um cilindro é como o perímetro da base do cilindro vezes a altura do cilindro.
O perímetro de um círculo é . Se é a altura do cilindro, a área fica assim:
Nós não temos o raio da base do cilíndro, mas temos o diâmetro . Como :
Substituindo os valores de e :
Passo 3
Agora podemos aplicar a fórmula da tensão cisalhante média:
Vimos no passo 1 que deve ser igual à e vimos no passo 2 que , então:
Para termos um resultado em , vamos reescrever como :
Fazendo a divisão, isso dá: