Duas pranchas de madeira, cada uma com de espessura e de largura são unidas pela junta de encaixe mostrada na figura. Sabendo que a madeira utilizada rompe por cisalhamento ao longo das fibras quando a tensão de cisalhamento média alcança , determine a intensidade da carga axial que romperá a junta.
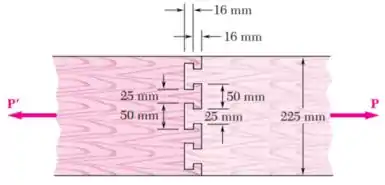
Passo 1
Existem conexões que estão resistindo ao cisalhamento gerado pela força :
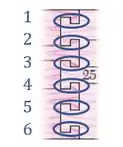
Observando uma dessas conexões de perto, conseguimos identificar uma seção resistente ao cisalhamento, como indicado pela linha tracejada na figura abaixo:
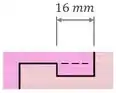
Cada uma dessas seções resistentes possui dimensões de :
- a dimensão de vem da figura original do exercício;
- e a de corresponde à espessura das pranchas de madeira.
Para o equilíbrio da prancha de madeira, cada uma dessas seções deve exercer uma força cisalhante interna de tal forma que a soma de todas as forças seja igual à força :
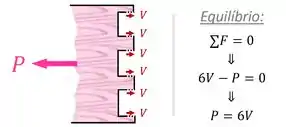
Entendido o que está acontecendo no exercício, vamos pensar agora em como resolvê-lo:
- O exercício quer saber o valor da força necessária para provocar uma falha nas juntas;
- Para encontrar , precisamos encontrar primeiro o valor da força de cisalhamento interna necessária para romper uma junta;
- pode ser encontrado usando a fórmula da tensão cisalhante média , uma vez que o exercício já nos disse que é necessário uma tensão para romper a madeira;
- Antes de usarmos a equação , só precisamos calcular antes a área da seção de dimensões .
Passo 2
Vamos começar então pelo cálculo das áreas !
Em uma prancha de madeira, existem seções resistentes ao cisalhamento.
Cada uma dessas seções possui dimensões de (comprimento da seção resistente) por (espessura da prancha de madeira).
Então, a área de uma dessas seções é dado por:
Passo 3
A tensão de falha da madeira foi fornecido pelo exercício e agora encontramos a área de uma seção resistente.
Então podemos calcular a força cisalhante interna de falha das juntas através da fórmula da tensão cisalhante média:
Substituindo os valores de e :
Isolando :
Como :
Passo 4
Como a força precisa provocar esforços internos nas juntas de uma prancha de madeira:
Se for necessário, um Diagrama de Corpo Livre e uma análise das condições de equilíbrio podem ser feitas para provar essa relação:
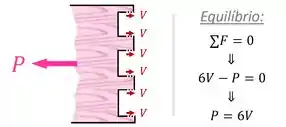
Como :
Reescrevendo em :