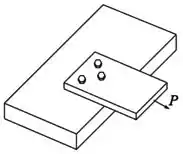
Uma placa é fixada a uma base de madeira por meio de três parafusos de diâmetro , conforme mostra a figura. Calcular a tensão média de cisalhamento nos parafusos para uma carga .
Passo 1
Temos uma situação de cisalhamento simples, em que três parafusos iguais de diâmetro estão resistindo juntos à carga .
O exercício pede a tensão de cisalhamento média nos parafusos. que deve ser encontrada pela sua fórmula:
Nos resta encontrar então a força cisalhante interna e a área da seção resistente à essa força .
Passo 2
Podemos interpretar como o esforço interno total, acumulado entre os três parafusos, e como a seção resistente total, acumulada entre os três parafusos.
Se é o esforço interno total, acumulado entre os três parafusos, ele deve resistir à toda a carga , de tal forma que:
E quanto à área ?
Bom, a área da seção transversal de um parafuso de diâmetro é dada pela área de um círculo: .
Então área da seção resistente total, acumulada entre os três parafusos, será 3 vezes isso:
Substituindo :
Passo 3
Agora, podemos inserir os valores que encontramos para e na equação da tensão cisalhante média:
Para conseguir um resultado em , reescrevemos como :