As componentes de madeira e devem ser unidas por cobrejuntas de madeira compensada que serão totalmente coladas às superfícies em contato. Como parte do projeto da junção, e sabendo que a folga entre as extremidades das componentes deve ser , determine o comprimento mínimo permitido para que a tensão de cisalhamento média na cola não exceda .
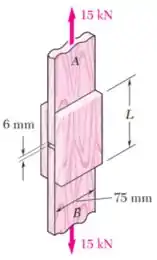
Passo 1
As madeiras tentam cisalhar (cortar) a cola, gerando uma uma força cisalhante interna na cola, e, consequentemente, uma tensão de cisalhamento média nela.
Quando excede , a cola falha e as madeiras se soltam.
Como reação ao esforço interno que as madeiras geram na cola, a cola faz forças de mesma intensidade nas madeiras. São essas forças que mantêm as madeiras juntas e em equilíbrio:
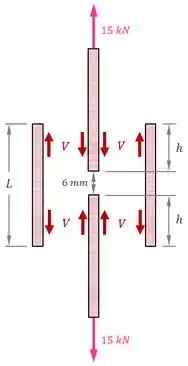
Como sempre, é a seção resistente à força cisalhante.
Pensa aí! A seção da cola resistente à essas forças é a área retangular na junção entre duas madeiras.
Essa área retangular possui base e altura , como mostram a figura original do exercício e a figura acima, respectivamente.
Para resolver o exercício vamos ter que:
- Calcular a força cisalhante interna na cola;
- Calcular a área da cola resistente à essa força . Essa área vai ser encontrada em função de para evitar muitos cálculos;
- Inserir esses valores na fórmula de tensão cisalhante média e aplicar a condição para encontrar o valor mínimo que deve ter;
- Usar a relação (retirada da figura acima) para finalmente encontrar o valor mínimo que deve ter.
Passo 2
Para calcular a força cisalhante interna , vamos observar o equilíbrio de uma madeira:

Todas as forças estão na vertical, então só precisamos fazer o equilíbrio de forças na vertical:
Como a força de aponta para cima e as forças apontam para baixo:
Vamos guardar esse valor!
Passo 3
Próximo passo é calcular a área da seção resistente de cola ao esforço interno .
Como a área é retangular:
Substituindo :
Passo 4
e calculados, hora da fórmula da tensão cisalhante média
Substituindo os valores encontrados para e :
Lembra aí! Queremos saber qual o valor mínimo de tal que . Então vamos aplicar essa condição:
Isolando :
Passo 5
Pausa para observar as unidades dessa última equação:
(Se quiser, pode fazer essa pausa em uma folha de rascunho!)
Lembra aí! Pascal () é o mesmo que newtons por metro quadrado ().
Então podemos substituir por :
Cortando com :
Arrumando as unidades:
Substituindo por :
Passo 6
Voltando para a nossa equação:
Como :
Calculando:
Ou seja, o valor mínimo de é .
Passo 7
Agora só falta aplicar a relação , como mostra a figura:
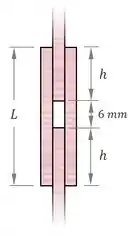
Aplicando essa relação e substituindo o valor mínimo de (), encontramos o valor mínimo de :