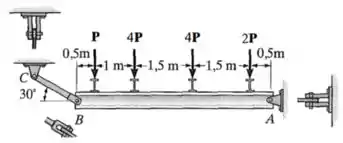
A viga é apoiada por um pino em e um elo curto . Se , determine a tensão de cisalhamento média desenvolvida nos pinos em , e . Todos os pinos estão sujeitos a cisalhamento duplo, como mostra a figura, e cada um tem diâmetro de .
Passo 1
Fala aí, galerinha! O problema pede para que calculemos as tensões cisalhantes dos pinos e ainda falou que trata-se de cisalhamento duplo. Vamos relembrar aqui que cisalhamento duplo tem a seguinte equação:
Onde é a força cortante.
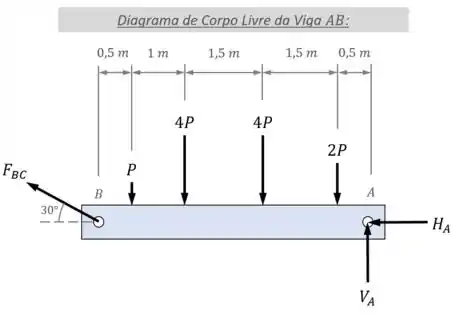
Show de bola! Mas precisamos entender também que a viga é mantida em equilíbrio pelas reações:
- do apoio (uma reação na vertical, , e uma na horizontal, );
- e da haste (uma força , no sentido da própria haste),
como mostra o seu Diagrama de Corpo Livre:
Passo 2
Aplicando as condições de equilíbrio nessa viga e sabendo que , conseguimos calcular o valor das reações , e .
Vamos começar aplicando as condições de equilíbrio no diagrama de corpo livre da viga:
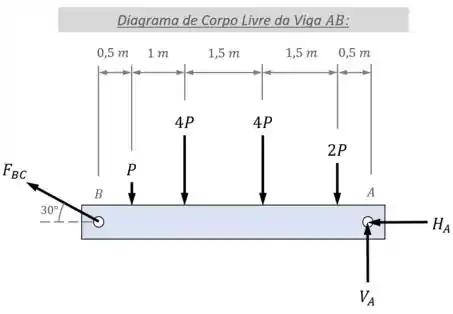
Lembra aí! As condições de equilíbrio possíveis são equilíbrio de forças (na vertical e na horizontal) e equilíbrio de momentos (em relação à algum ponto).
Como temos incógnitas (, e ), condições de equilíbrio são o suficiente!
Vamos fazer o equilíbrio de momentos em relação ao ponto (vamos fazer isso para poder eliminar a força e ficar mais fácil o cálculo, já que não gera momento em ) e o equilíbrio de forças nas duas direções.
Começando pelo equilíbrio de momentos:
Em relação ao ponto , só as cargas e a força geram momentos e os braços dessas forças podem ser vistos no DCL acima. Além disso, só a força gera um momento no sentido anti-horário.
Tendo tudo isso em mente, o somatório de momentos fica assim:
Somando todas as forças :
Isolando :
Uma incógnita descoberta, faltam duas!
Agora podemos partir para o equilíbrio de forças na vertical:
Tomando o devido cuidado de decompor a força , esse somatório de forças fica assim:
Somando as forças :
Como e :
Isolando :
e descobertas, agora só falta encontrar .
Finalmente, temos o equilíbrio de forças na horizontal:
Mais uma vez tomando o cuidado de decompor , esse somatório de forças fica assim:
Isolando e substituindo :
Como :
Passo 3
Reações descobertas! Antes de calcular as tensões em cada pino, vamos só calcular a área da seção transversal dos pinos.
Por se tratar de uma seção circular de diâmetro :
Passo 4
Agora podemos calcular as tensões em cada pino. Vamos olhar o pino isoladamente para entender o que está acontecendo:
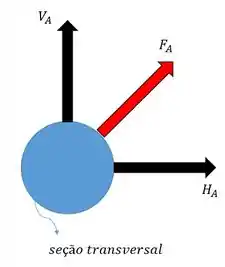
Olha como as duas forças e atuam no plano da seção transversal. Isso faz com que ambas contribuam para a tensão de cisalhamento. Então podemos juntar as duas numa força só
Juntas, as duas reações em formam uma força , que é a força a qual o pino em está sujeito sob cisalhamento duplo.
A tensão cisalhante média nesses pinos é dada pela sua fórmula:
Ou seja, para o pino em vamos ter:
Para todos os pinos, a área da seção transversal é a mesma e vai ser calculada a partir de seu diâmetro .
Para o pino em , precisamos primeiro calcular a força resultante nesse ponto. Como temos duas forças e perpendiculares, usamos o teorema de pitágoras:
Substituindo e :
Aplicando a fórmula da tensão cisalhante média para o pino em , que está sob cisalhamento duplo de tal forma que , temos:
Substituindo , e :
Para obtermos resultados em , podemos reescrever como :
Calculando, isso dá:
Passo 5
Para os pino em e , já temos o valor da força que atua neles. Da mesma forma que o pino a força vai ser a própria força da fórmula:
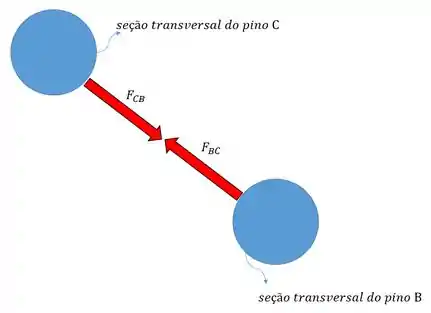
Pessoal, o pino e o pino têm a mesma força atuando e possuem a mesma área. Logo estão sujeitos à mesma tensão cisalhante .
Aplicando a fórmula da tensão cisalhante média , tendo em mente que esses pinos estão sob cisalhamento duplo de tal forma que , temos:
Substituindo , :
Vemos que essa é a mesma conta de , então já podemos adiantar que: