A conexão mostrada na figura consiste de cinco placas de aço, cada uma com de espessura, unidas por um único parafuso de de diâmetro. A carga total transferida para as placas é , distribuída entre as placas como mostrado.
Calcule a maior tensão de cisalhamento agindo contra o parafuso.

Passo 1
Nesse exercício várias forças diferentes estão atuando no parafuso, fazendo com que a força cisalhante interna varie ao longo das seções do parafuso.
Precisamos avaliar as diferentes seções do parafuso (entre a 1ª e a 2ª placa, entre a 2ª e a 3ª, etc.) para encontrar o maior esforço interno .
Com isso, poderemos calcular a maior tensão de cisalhamento agindo contra o parafuso.
Vamos fazer uma resolução em partes:
- Fazer um Diagrama de Corpo Livre do parafuso e avaliar as suas seções para encontrar a maior força cisalhante interna, ;
- Calcular a área da seção transversal do parafuso usando o diâmetro ;
- Usar a fórmula da tensão cisalhante média para encontrar a maior tensão cisalhante, .
Passo 2
Começando pelo Diagrama de Corpo Livre:
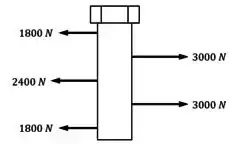
A partir desse diagrama, conseguimos identificar as diferentes seções transversais do parafuso que podem ter valores distintos de , como feito abaixo com as linhas tracejadas:
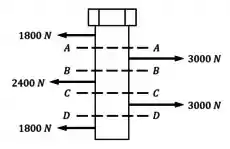
Feito o Diagrama de Corpo Livre, o próximo passo é fazer a análise dos esforços internos nas diferentes seções:
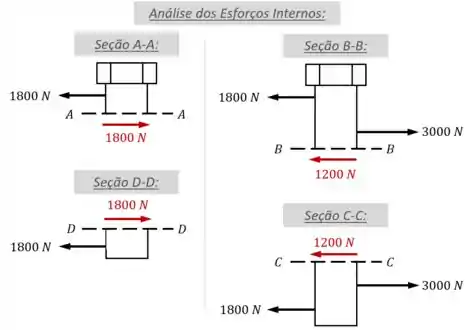
Dessa análise, tiramos que a intensidade máxima da força cisalhante interna é igual à intensidade dessa força nas seções e :
Passo 3
Já temos , o que significa que estamos perto de encontrar .
Antes disso, vamos só calcular o valor da área da seção transversal.
A seção transversal do parafuso é circular. Lembra aí... A área do círculo pode ser dada em função do seu diâmetro pela fórmula:
Substituindo :
Passo 4
Usando a força cisalhante interna máxima na equação da tensão cisalhante máxima , encontramos :
Substituindo e :
Como :
E assim obtemos nosso resultado: