- Calcule o equivalente Thévenin para o circuito externo ao resistor para o circuito:
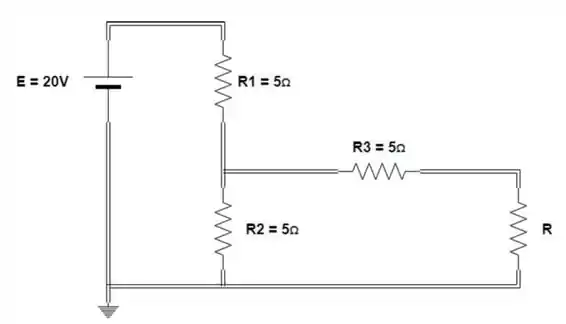
- Calcule a potência fornecida para quando os valores de forem 2Ω e 100Ω.

Passo 1
Primeiro vamos calcular a resistência Thévenin do circuito vista pelo resistor . Para isso, vamos substituir as fontes de tensão independentes por curto circuitos:
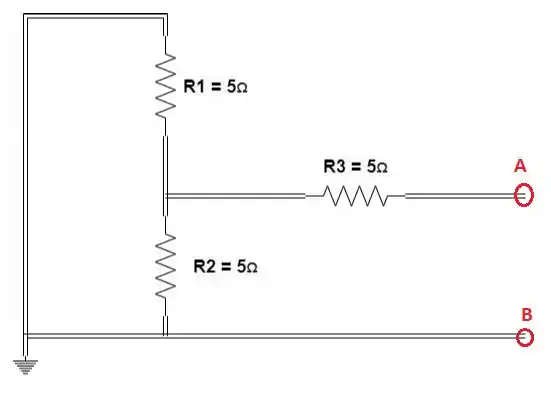
Se formos medir a resistência Thévenin, percebemos que o resistor está em paralelo com o resistor :
Essa resistência equivalente está em série com o resistor , logo o
Passo 2
Para calcular a tensão em cima do resistor , vamos abrir o circuito e retirar o resistor e verificar qual a tensão aplicada a ele:
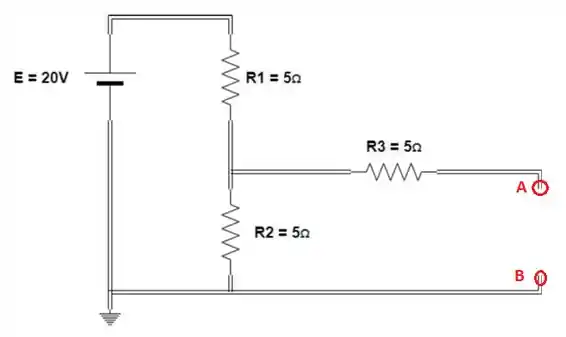
Como o circuito está aberto entre os pontos A e B, não circula corrente pelo resistor , assim a tensão entre os pontos A e B pode ser medida pela queda de tensão em cima do resistor .
Passo 3
Para medir a tensão em cima do resistor , podemos realizar um divisor de tensão:
Passo 4
Logo, podemos desenhar o circuito como:
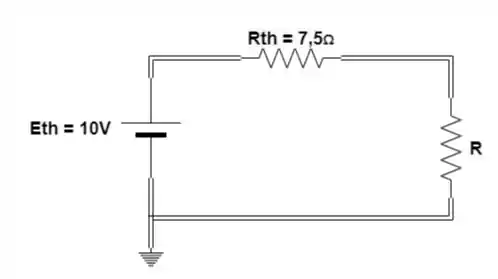
Passo 5
Para fazer os cálculos da letra b, devemos substituir primeiro. Como está em série com o :
A corrente que circula pelos resistores é:
Logo a potência dissipada é igual a:
Passo 6
Substituindo primeiro. Como está em série com o :
A corrente que circula pelos resistores é:
Logo a potência dissipada é igual a:
Resposta
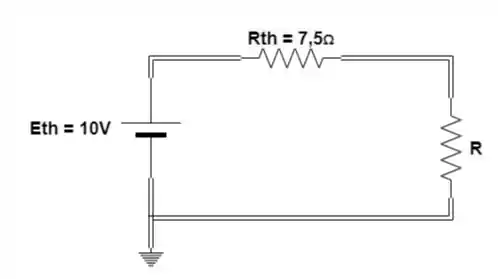
- e